Question

The smallest circle with a center on the $y$- axis and passing through the point $\left( 7,3 \right)$ has radius.

Answer 1

For these kind of questions, we need to make use of the standard equation of the circle which is $a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+c=0$ , where $a=b$ . Generally we take $a=b=1$ . So let us take it here. So the standard form of the equation of the circle which we will be using in this question is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ . The center of the circle from the standard equation would be $\left( -g,-f \right)$. Since it is specified in the question that the center is on the $y$- axis, $-g=0$ .

Complete step by step answer:
Since it is specified in the question that the center is on the $y$- axis, $-g=0$. Let us substitute in the standard equation.
Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+2\left( 0 \right)x+2fy+c=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+2fy+c=0 \\\ \end{aligned}$
Now we are given an extra piece of information. This circle passes through the point $\left( 7,3 \right)$ . So let us substitute. Then we will find a relation between $f,c$ . Using that relation and some rules of differentiation, we will find the radius of the smallest circle.
Upon substituting, we get the following:
$\begin{aligned} & \Rightarrow {{x}^{2}}+{{y}^{2}}+2fy+c=0 \\\ & \Rightarrow {{\left( 7 \right)}^{2}}+{{\left( 3 \right)}^{2}}+2\times f\times 3+c=0 \\\ & \Rightarrow 49+9+6f+c=0 \\\ & \Rightarrow 6f+c=-58...eqn\left( 1 \right) \\\ \end{aligned}$
We got a relation between both the variables.
The formula for calculating radius of a circle is $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$. Since $g=0$ , let us substitute. We will also substitute $c$ in terms of $f$ using $eqn\left( 1 \right)$ .
Upon doing so, we get the following :
$r=h\left( f \right)=\sqrt{{{f}^{2}}+6f+58}$ .
We got $r$ as a function of $f$. That is why we wrote $h\left( f \right)$ .
Let us use the first rule of differentiation. The first rule of differentiation is that we can equate the first derivative of a function to $0$.
Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow r=h\left( f \right)=\sqrt{{{f}^{2}}+6f+58} \\\ & \Rightarrow \dfrac{dr}{df}=\dfrac{1}{2\sqrt{{{f}^{2}}+6f+58}}\left[ 2f+6 \right]=0 \\\ \end{aligned}$
$\sqrt{{{f}^{2}}+6f+58}$ cannot be $0$ since it is in the denominator. So only $2f+6=0$ .
Let us solve that and get the value.
Upon solving , we get the following :
$\begin{aligned} & \Rightarrow 2f+6=0 \\\ & \Rightarrow f=-3 \\\ \end{aligned}$
So $f$ is $-3$ , the value of $c$ from $eqn\left( 1 \right)$ would be the following :
$\begin{aligned} & \Rightarrow 6f+c=-58 \\\ & \Rightarrow c=-40 \\\ \end{aligned}$
So the radius of the smallest possible circle is :
$\begin{aligned} & \Rightarrow r=\sqrt{{{g}^{2}}+{{f}^{2}}-c} \\\ & \Rightarrow r=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( -3 \right)}^{2}}-\left( -40 \right)}=\sqrt{49}=7 \\\ \end{aligned}$
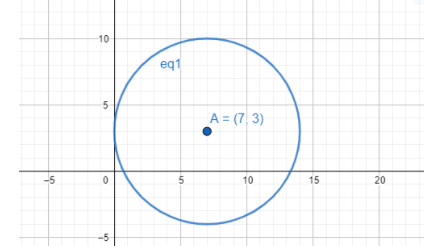
$\therefore$ The smallest circle with center on the $y$- axis and passing through the point $\left( 7,3 \right)$ has a radius $7$ .
Graph for reference :

Note: After we got the value of $f$ after differentiating and equating it to zero, we can also go for the second rule of differentiation to specify whether that particular $f$ value gives us the maximum or minimum. But since only one value is obtained, we can say for sure that this value that we got would give us the radius of the smallest. If there are $2$, we should go for a second rule of differentiation as one value can give us the radius of the largest circle possible while the other can give us the radius of the smallest circle possible.