Question

The slope of the straight line which does not intersect the $x - axis$ is equal to
\eqalign{ & 1)\dfrac{1}{2} \cr & 2)1 \cr & 3)\sqrt 3 \cr & 4)0 \cr}

Answer 1

Hint : The question is asking about the slope. A slope is also called the gradient of a line, it measures the steepness of the line. The question also mentions the straight line which is parallel to $x - axis$. The question asks about the slope of a line which does not intersect the $x - axis$ So, we will find out the type of the line and then find out the slope of that line.

Complete step-by-step answer :
The line is not supposed to intersect the $x - axis$. This means that the given line will be parallel to $x - axis$. Now, if we will find the slope of $0$. But we know that the slope of $x - axis$ is $0$. Since the given line is parallel to $x - axis$, the slope of that line will also be $0$.
This can be seen in the following graph.

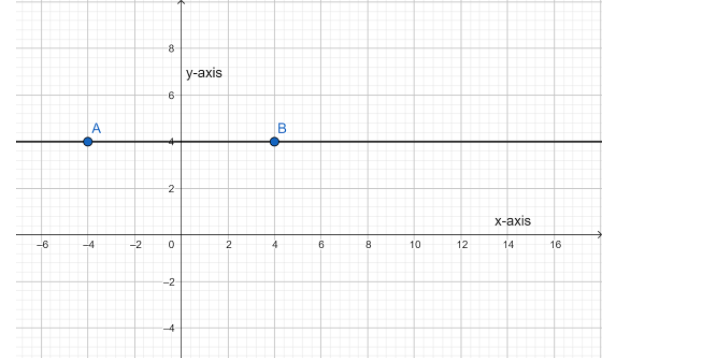
The line $\overleftrightarrow {AB}$ is parallel to the $x - axis$. And from the figure, we observe that the slope cannot be calculated. So, it is $0$
Hence, option (4) is the correct answer.
So, the correct answer is “Option 4”.

Note : It is important to read the question properly. The key word in the question would be, ‘Parallel to $x - axis$’, from this clue, figure out the type of the line. Only after we find out what type of line it is, we can move ahead to find out the slope. Do not forget that the slope will be zero for parallel lines.