Question

The slope of the line touching both the parabolas ${{y}^{2}}=4x$ and ${{x}^{2}}=-32y$ , is
(a) $\dfrac{1}{2}$
(b) $\dfrac{3}{2}$
(c) $\dfrac{1}{8}$
(d) $\dfrac{2}{3}$

Answer 1

First, before proceeding for this, we must draw the two parabolas and the line which touches them as a tangent to get the slope. Then, by substituting the value of y from the above equation of line in the equation of parabola given as ${{x}^{2}}=-32y$ . Then, the condition given in the question that the line touches both the parabolas in the fourth quadrant states that it will give the real values after solving the above equation. Then, by using this fact, we know for the quadratic equation, the discriminate which is ${{b}^{2}}-4ac$ for the equation $a{{x}^{2}}+bx+c=0$ must be zero and get the desired answer.

Complete step-by-step answer:
In this question, we are supposed to find the slope of the line touching both the parabolas ${{y}^{2}}=4x$ and ${{x}^{2}}=-32y$ .
So, before proceeding for this, we must draw the two parabolas and the line which touches them as a tangent to get the slope as:

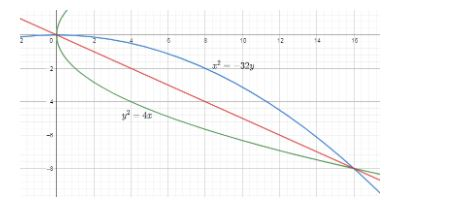
Now, b y using the equations of the parabolas given in the question, we will substitute the value of y from the study of the line equation where m is slope and $\dfrac{1}{m}$ is intercept which is given by:
$y=mx+\dfrac{1}{m}$
Now, by substituting the value of y from the above equation of line in the equation of parabola given as ${{x}^{2}}=-32y$ , we get:
${{x}^{2}}=-32\left( mx+\dfrac{1}{m} \right)$
So, by solving the above expression, we get:
$\begin{aligned} & {{x}^{2}}=-32mx-\dfrac{32}{m} \\\ & \Rightarrow {{x}^{2}}+32mx+\dfrac{32}{m}=0 \\\ \end{aligned}$
Then, the condition given in the question that the line touches both the parabolas in the fourth quadrant states that it will give the real values after solving the above equation.
So, by using this fact, we know for the quadratic equation, the discriminate which is ${{b}^{2}}-4ac$ for the equation $a{{x}^{2}}+bx+c=0$ must be zero.
So, by applying the same for the above found expression, we get:
${{\left( 32m \right)}^{2}}-4\left( \dfrac{32}{m} \right)=0$
Then, by solving the above expression, we get:
$\begin{aligned} & {{\left( 32m \right)}^{2}}=4\left( \dfrac{32}{m} \right) \\\ & \Rightarrow 32{{m}^{3}}=4 \\\ & \Rightarrow {{m}^{3}}=\dfrac{4}{32} \\\ & \Rightarrow {{m}^{3}}=\dfrac{1}{8} \\\ & \Rightarrow m=\dfrac{1}{2} \\\ \end{aligned}$
So, we get the value of the slope of the line as $\dfrac{1}{2}$ .

So, the correct answer is “Option A”.

Note: Now, to solve these type of the questions we need to know some of the basic conditions for the roots of the equation $p{{x}^{2}}+qx+r=0$ is given as:
Roots of the equation are imaginary if $\sqrt{{{q}^{2}}-4pr}<0$ .
Roots of the equation are real and equal if $\sqrt{{{q}^{2}}-4pr}=0$ .
Roots of the equation are real and distinct if $\sqrt{{{q}^{2}}-4pr}>0$ .