Question
Question: The slope of tangents drawn from a point (4, 10) to the parabola \({y^2} = 9x\)are \( A.{\text...
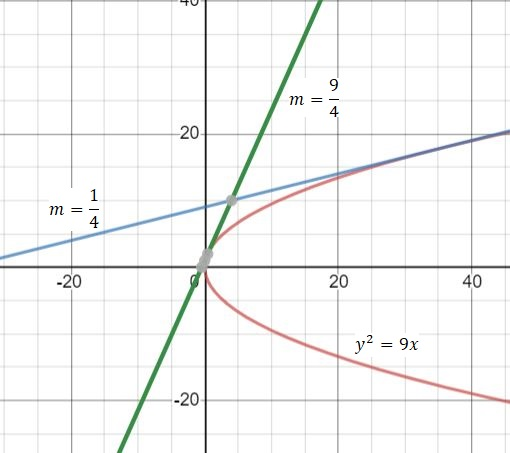
The slope of tangents drawn from a point (4, 10) to the parabola y2=9xare
A. 41,43 B. 49,41 C. 31,41 D.Noneofthese
Solution
Hint: - Here we go through by the general term of parabola i.e. y2=4ax .As we know the equation of tangent to this parabola isy=mx+ma. So simply put the values and then find the value of m to get the slopes.
Complete step-by-step solution -
Here in the question the given parabola is y2=9x if we compare this parabola with the general form of parabola we get, 4a=9 i.e. a=49.
We know that the equation of tangent to the parabola y2=4ax isy=mx+ma.
After putting the values of ‘a’ in tangent equation we get, y=mx+4m9
And in the question it is given that the tangent is passing from the point (4, 10) so this point should satisfy in the tangent equation,
I.e. 10=4m+4m9 after solving this equation we get the value of m.
⇒16m2−40m+9=0 ⇒16m2−4m−36m+9=0 ⇒4m(4m−1)−9(4m−1)=0 ⇒(4m−1)(4m−9)=0
∴m=41,49 This is the required slope of the tangent as we know in the tangent equation m represents a slope.
Hence, option B is the correct answer.
Note:- Whenever we face such a type of question the key concept for solving the question is compare the parabola equation with the general form of parabola to find the value of a. Here it is the question on tangent so we write the general equation of tangent on general form of parabola, then put the value of ‘a’ to find the equation of tangent to the parabola that is given in the question. And then put the points from where the tangent is passing by these steps so we can find out the slope of the tangent.
