Question

The slope of any line which is parallel to x-axis is …………. .
A.0
B.1
C.-1
D.2

Answer 1

Hint: In this question we are asked to find the slope of a straight line which is parallel to x-axis. But, here we didn’t get any coordinates or equations in the question. So, we will try to find it by drawing a straight line on the graph and find the slope by using formula of $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ to get the answer.

Complete step-by-step answer:
Here, we need to find the slope of any line which is parallel to x-axis.
Let us draw a straight line AB on the graph which is parallel to x-axis.

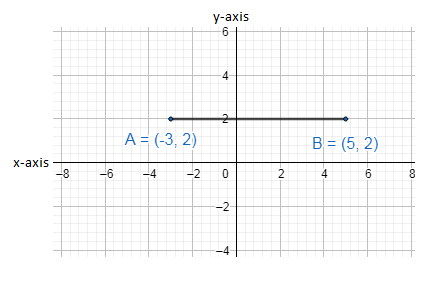
In this graph, the horizontal line is x-axis and the vertical line is y-axis.
By drawing the straight line on the graph we get two points A and B where $\left( {{x}_{1}},{{y}_{1}} \right)$is A$\left( -3,2 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is B$\left( 5,2 \right)$ .
Now, we can find the slope of the straight line parallel to the x-axis by taking A and B in the formula of slope.
i.e. $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Put, $A=\left( {{x}_{1}},{{y}_{1}} \right)=\left( -3,2 \right)$ and $B=\left( {{x}_{2}},{{y}_{2}} \right)=\left( 5,2 \right)$
$\begin{aligned} & \text{slope}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \\\ & =\dfrac{2-2}{5-\left( -3 \right)} \\\ & =\dfrac{0}{8} \\\ & =0 \\\ \end{aligned}$
By this we get to know that the slope of any straight line parallel to the x-axis is 0.
Therefore, option (a) is the correct answer.
Note: Generally students get confused while solving such types of questions and they may make mistakes while taking x and y coordinates. They should know that y coordinates of the straight line parallel to x-axis will always be the same. Students can solve this problem logically. The slope of a straight line parallel to the x-axis will always be ‘0’ as there will be no slope to the straight line which is parallel to the axis.