Question

The slope of a Normal stress vs. linear strain in the linear region of the graph for a copper wire gives us
A. Young’s modulus
B. Rigidity modulus
C. Bulk’s modulus
D. Poisson’s ratio

Answer 1

In the question we are given a normal stress vs. normal strain graph and are asked what does the slope of the graph give. We know the shape of a normal stress vs. linear strain graph; hence we know how to find the slope of the curve. We can compare the slope with given options and thus we can find the solution.

Complete answer:
We are given a graph of normal stress vs. linear strain.
First let us see what normal stress is.
When the direction of the deforming force applied to the surface of an object is perpendicular to the surface or is normal to the surface, the stress generated by the surface of the body is said to be normal stress.
Linear strain or normal strain is the ratio of the change in dimension of the body due to the deforming force applied perpendicular to the surface to the original dimension of the body.
Here we consider the graph of normal stress and normal strain.

The figure below shows the graph of normal stress vs. linear strain.

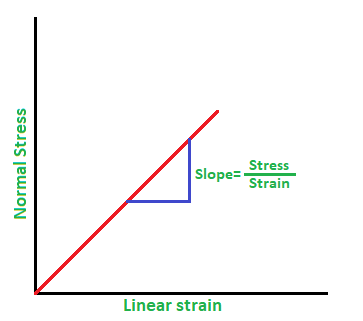
We know that the graph is a straight line.
Since it is a straight line, we can find the slope of the line as,
$\text{slope=}\dfrac{\text{stress}}{\text{strain}}$
We know that this is the formula of Young’s modulus, i.e.
$\text{Young }\\!\\!'\\!\\!\text{ s modulus=}\dfrac{\text{stress}}{\text{strain}}$
From this we can conclude that the slope of a normal stress vs. linear strain graph gives Young’s modulus.

So, the correct answer is “Option A”.

Note:
We know that stress is defined as the restoring force experienced per unit area of the surface. When we apply a deforming force to a surface, the surface deforms. In such a situation the surface will generate a restoring force to attain its original shape. This restoring force which is equal and opposite to the force applied to the surface is known as stress.
The equation for stress is given as,
$\sigma =\dfrac{F}{A}$, where ‘$\sigma$’ is the stress, ‘F’ is the force applied and ‘A’ is the cross sectional area.
Strain is simply defined as the change in the shape of an object when we apply a deforming force to the object.
The equation for strain is given as,
$strain=\dfrac{\Delta L}{L}$, where ‘$\Delta L$’ is the change in dimension and ‘L’ is the original dimension.