Question

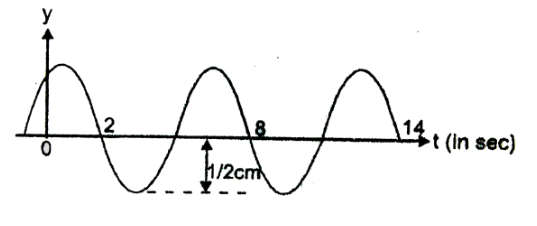
The sketch in the figure shows the displacement time curve of a sinusoidal wave at $x = 8m$ . Taking the velocity of the wave $v = 6m{s^{ - 1}}$ along the positive X-axis, write the equation of the wave.
(A) $y = 0.5\sin \left( {\dfrac{\pi }{3}t + \dfrac{\pi }{{18}}x + \dfrac{{7\pi }}{9}} \right)$
(B) $y = 0.5\sin \left( {\dfrac{\pi }{3}t + \dfrac{\pi }{{18}}x + \dfrac{{11\pi }}{9}} \right)$
(C) $y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \dfrac{{11\pi }}{9}} \right)$
(D) $y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \dfrac{{7\pi }}{9}} \right)$

Answer 1

Hint : Use the general equation of a sinusoidal wave and find the different parameters of the wave. The general equation of a sinusoidal wave propagating along positive X-direction is given by, $y = A\sin \left( {\omega t - kx + \varphi } \right)$ . Where, $A$ is the amplitude of the wave, $\omega$ is the angular frequency of the wave, $k$ is the propagation constant of the wave, $\varphi$ is the initial phase, $x$ is the position of the wave and $t$ is the time.

Complete Step By Step Answer:
We know that the equation of a sinusoidal wave propagating along positive X- direction is given by, $y = A\sin \left( {\omega t - kx + \varphi } \right)$ . Where, $A$ is the amplitude of the wave, $\omega$ is the angular frequency of the wave, $k$ is the propagation constant of the wave, $\varphi$ is the initial phase. $x$ is the position of the wave and $t$ is the time.
From the figure we can see that at $t = 2s$ to $t = 8s$ the wave completes one single oscillation. Now we know, the time period of a wave is the time required to complete one complete oscillation is called the time period of the wave. Hence the time period of the wave will be, $T = (8 - 2) = 6s$ .
Now, we know that the frequency of a wave is the total number of complete oscillation in one second.
Hence, frequency of the wave will be, $f = \dfrac{1}{T} = \dfrac{1}{6}Hz$ .
So, the angular frequency of the wave will be, $\omega = 2\pi f$ .
Putting the values we get, $\omega = 2\pi \dfrac{1}{6} = \dfrac{\pi }{3}rad/s$
Now, From the figure we can see that the amplitude of the wave is , $A = 0.5cm = 5 \times {10^{ - 3}}m$ .
Now we know that the propagation constant of the wave is related to the wavelength of the wave as, $k = \dfrac{{2\pi }}{\lambda }$ . And we know, wavelength of wave is the distance covered in one complete oscillation , $\lambda = \dfrac{v}{f}$ where $v$ is the velocity of the wave.
We have given here that the velocity of the wave is, $v = 6m{s^{ - 1}}$ and we have found $f = \dfrac{1}{6}Hz$ .
Putting the values we get, $\lambda = \dfrac{6}{{\dfrac{1}{6}}} = 36m$ .
Hence propagation constant will be, $k = \dfrac{{2\pi }}{\lambda } = \dfrac{{2\pi }}{{36}} = \dfrac{\pi }{{18}}{m^{ - 1}}$
So, putting these values in the sinusoidal wave equation we get the wave equation as,
$y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \varphi } \right)$ [Taking displacement in $cm$ ]
Since, there is insufficient data to find the initial phase of the wave we have to check the available options.
Now, putting, $\varphi = \dfrac{{11\pi }}{9}$ at $t = 0$ and $x = 8$
we get, $y = 0.5\sin (0 - \dfrac{{8\pi }}{{18}} + \dfrac{{11\pi }}{9})$
Or, $y = 0.5\sin (\dfrac{{7\pi }}{9}) = 0.321$
So, putting $\varphi = \dfrac{{7\pi }}{9}$ at $t = 0$ and $x = 8$
We get, $y = 0.5\sin (0 - \dfrac{{8\pi }}{{18}} + \dfrac{{7\pi }}{9})$
Or, $y = 0.5\sin (\dfrac{\pi }{3}) = 0.433$
From observation of the graph we can see that the value of $y$ t $t = 0$ and $x = 8$ must be near the $y \geqslant 0.4cm$ range. Hence, $\varphi = \dfrac{{7\pi }}{9}$ must be the initial phase.
So, equation of the wave will be, $y = 0.5\sin \left( {\dfrac{\pi }{3}t - \dfrac{\pi }{{18}}x + \dfrac{{7\pi }}{9}} \right)$
So, Option (D) is correct.

Note :
$\bullet$ Here, if the value of the amplitude of the wave at $t = 0s$ was given we could find the initial phase of the wave directly.
$\bullet$ The equation of standing waves always has a fixed value of $x$ . The figure of the wave given here is a standing wave since, only the variation of the displacement of the wave with time is given at $x = 8m$ , but it is not actually a standing wave since it is told that the wave is propagating along the positive X-axis.