Question
Question: The simple pendulum A of mass \({{m}_{A}}\) and length l is suspended from the trolley B of mass \({...
The simple pendulum A of mass mA and length l is suspended from the trolley B of mass mB. If the system is released from rest at θ=0, determine the velocity vB of the trolley and tension in the string when θ=90∘. Friction is negligible.
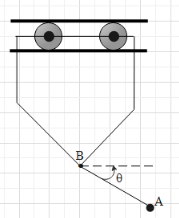
Solution
The net force on the system in horizontal direction is zero. Therefore, use the law of conservation of momentum. Then use the work energy theorem, where the work done by the gravity is equal to the change in the kinetic energy of the system.
Formula used:
W=mgh
where W is the work done by gravity on a mass m when it comes down from height h. g is acceleration due to gravity.
K=21mv2
where K is the kinetic energy of mass m travelling with speed v.
P=mv
where P is momentum.
Complete step by step answer:
The net force acting on the given system is the gravitational force Fg=mAg (acting on the bob of the pendulum). Due to the gravitational force, the bob will come down and the trolley will move in front.From the work-energy theorem we know that the total work done on a system is equal to the change in its kinetic energy. i.e. W=ΔK.
Here, the work done on the system is,
W=mAgl …. (i), when θ=90∘.
Let the kinetic energy of the bob and the trolley be, KA=21mAvA2 and KB=21mBvB2.
Since the system was at rest initially, ΔK=KA+KB.
ΔK=21mAvA2+21mBvB2 ….. (ii).
Now, equate (i) and (ii).
mAgl=21mAvA2+21mBvB2 …. (iii).
The net force on the system in the horizontal direction is zero. This means that the momentum of the system in the horizontal direction is constant. Initially momentum of the system is zero. And when θ=90∘, the trolley and the bob are moving in opposite directions.Therefore, we can say that mAvA=mBvB.
vA=mAmBvB
Substitute this value in (iii).
⇒mAgl=21mA(mAmBvB)2+21mBvB2
⇒mAgl=21mAmB2vB2+21mBvB2
⇒2mA2gl=mB2vB2+mAmBvB2
⇒vB2=mB2+mAmB2mA2gl
∴vB=mB2+mAmB2mA2gl
Note: You may be wondering if the gravitational force is acting on the bob and as a result it is accelerating. However, the gravitational force on the trolley is balanced by the normal reaction. Then how it is being accelerated. It is due to the third law of motion, which says that every action has an equal and opposite reaction.As the bob comes down, it exerts a force on the trolley and in return the trolley exerts a force on the bob of equal magnitude but opposite in direction.The work done by the reaction forces add up to zero.
