Question

The sides of rhombus ABCD are parallel to the line x – y + 2 = 0 and 7x – y + 3 = 0. If the diagonals of the rhombus intersect at P ( 1, 2 ) and the vertex A ( different form the origin ) is on the y – axis, then the ordinates of A is
( a )2
( b )$\dfrac{7}{4}$
( c ) $\dfrac{7}{2}$
( d ) $\dfrac{5}{2}$

Answer 1

To solve this question, we will first find the equation of angle bisector using condition $\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}}}=\pm \dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{{{a}_{2}}^{2}+{{b}_{2}}^{2}}}$. From where we will get, two lines of which we will find the slopes then, we will find slope of point A to point P and hence, then will solve for the value of a.

Complete step-by-step answer:
Now, we know that the condition of two lines to be parallel if their slopes are the same is that if slope on line is l and slope of another line is m, then both lines are parallel if l = m.
Now, let we have two lines say ${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0$ and ${{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0$, then equation of angle bisector is $\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}}}=\pm \dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{{{a}_{2}}^{2}+{{b}_{2}}^{2}}}$
So, for parallel lines, x – y + 2 = 0 and 7x – y + 3 = 0, we get
$\dfrac{x\text{ }\text{ }y\text{ }+\text{ }2}{\sqrt{{{1}^{2}}+{{1}^{2}}}}=\pm \dfrac{7x\text{ }\text{ }y\text{ }+\text{ }3\text{ }}{\sqrt{{{7}^{2}}+{{(-1)}^{2}}}}$
$\dfrac{x\text{ }\text{ }y\text{ }+\text{ }2}{\sqrt{2}}=\pm \dfrac{7x\text{ }\text{ }y\text{ }+\text{ }3\text{ }}{5\sqrt{2}}$
For, positive we get
$\dfrac{x\text{ }\text{ }y\text{ }+\text{ }2}{1}=+\dfrac{7x\text{ }\text{ }y\text{ }+\text{ }3\text{ }}{5}$
$5x\text{ }\text{ 5}y\text{ }+\text{ 10}=7x\text{ }\text{ }y\text{ }+\text{ }3$
On solving we get line
2x + 4y – 7 = 0
For, negative we get
$\dfrac{x\text{ }\text{ }y\text{ }+\text{ }2}{1}=-\dfrac{7x\text{ }\text{ }y\text{ }+\text{ }3\text{ }}{5}$
$5x\text{ }\text{ 5}y\text{ }+\text{ 10}=-(7x\text{ }\text{ }y\text{ }+\text{ }3)$
On solving we get line
12x – 6y + 13 = 0
Now, the standard equation of line is y = mx + c, where m is slope of line.
So, we can write 3x + 4y – 7 = 0 as $y=-\dfrac{x}{2}+\dfrac{7}{4}$
So, slope of line 3x + 4y – 7 = 0 is $-\dfrac{1}{2}$
Similarly, we can write 12x – 6y + 13 = 0 as $y=-\dfrac{x}{2}+\dfrac{7}{4}$
So, the slope of line 12x – 6y + 13 = 0 is 2.
Now, we have to find the ordinate of A.
So, let point be A ( 0,a ) as it is on y – axis.

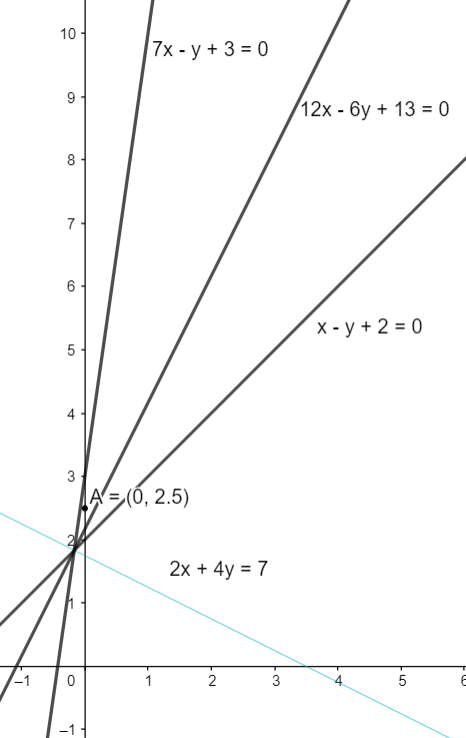
Then, slope of A ( 0, a ) to the point P ( 1,2 ) will be $\dfrac{2-a}{1-0}=2-a$ , as slope is given as $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Now if slope of A ( 0, a ) to the point P ( 1,2 ) will be equal to slope of line 12x – 6y + 13 = 0, then
2 – a =2
a = 0, which is not possible as it lies on y – axis.
So, only case left is $2-a=-\dfrac{1}{2}$
On solving, we get
$a=\dfrac{5}{2}$
So, the correct answer is “Option d”.

Note: To solve this question, we need to know the relation of the slope of two lines which are parallel, that is slope of parallel lines are equal. Now, as in this question it is given that A lies on y – axis, so always remember that point A will be formed ( 0, a ) as point of x coordinate will be zero on y – axis.