Question

The sides of a triangle touch a parabola, and two of its angular points lie on another parabola with its axis in the same direction; prove that the locus of the third angular point is another parabola.

Answer 1

Hint: The sides, when extended touch the parabola. Assume the parabola being touched is ${{y}^{2}}=4ax$. Angular points are the same as vertices of the triangle, and the axis of the other parabola in the same direction means that it is the same as the parabola being touched, just with a different vertex and size of the lateral recta, and the positioning of the focus. In other words, the parabola is a bit shifted, and hence can be assumed to have the formula ${{y}^{2}}=4b(x+c)$. Assume the two vertices of the triangle lie on this second parabola, and proceed.

Complete step-by-step solution -

Let’s assume the parabola that the sides touch is ${{y}^{2}}=4ax$. The vertex of this parabola is (0,0) and its axis is the $x$ axis.
Let the triangle being talked about here be of the name triangle$ABC$. Let’s also assume that points $B$ and $C$ already lie on the other parabola with its axis in the same direction, and the locus of $A$ is what we have to find.
First of all, let’s find the general equation of the parabola that $B$ and $C$ might lie on. We know that the axis of this parabola is the same as that of ${{y}^{2}}=4ax$, which means the axis is the $x$ axis. Let’s assume it has its vertex at a point $(-c,0)$ and has its focus at a point $(b,0)$. This means, that the parabola that $B$ and $C$ lie on has the equation : ${{y}^{2}}=4b(x+c)$ since this parabola has its axis on the $x$ axis, in the same direction, and since we’ve kept both $b$ and $c$ as variable, it doesn’t point to one particular parabola.
Moving on, let’s come to the part where it says that the sides of the triangle $ABC$touch the parabola ${{y}^{2}}=4ax$. This means that the sides act as tangents to the parabola, and the vertices of the triangle, $A$, $B$ and $C$ are the intersection points of those very tangents.
In a parabola, the intersection point of the tangents drawn at two points lying on the parabola, with parameters ${{t}_{1}}$ and ${{t}_{2}}$ = $(a{{t}_{1}}{{t}_{2}},a({{t}_{1}}+{{t}_{2}}))$.
Let’s assume that $B$ is the intersection point of tangents drawn at points on the parabola with parameters ${{t}_{1}}$ and ${{t}_{2}}$.
This means that the coordinates of $B$ = $(a{{t}_{1}}{{t}_{2}},a({{t}_{1}}+{{t}_{2}}))$.
Let’s assume that $C$ is the intersection point of tangents drawn at points on the parabola with parameters ${{t}_{2}}$ and ${{t}_{3}}$.
This means that the coordinates of $C$ = $(a{{t}_{3}}{{t}_{2}},a({{t}_{3}}+{{t}_{2}}))$.
Let’s assume that $A$ is the intersection point of tangents drawn at points on the parabola with parameters ${{t}_{1}}$ and ${{t}_{3}}$.
This means that the coordinates of $A$ = $(a{{t}_{1}}{{t}_{3}},a({{t}_{1}}+{{t}_{3}}))$.
Since we assumed that $B$ and $C$ lie on the parabola ${{y}^{2}}=4b(x+c)$, they have to satisfy this equation.
Substituting $B$’s coordinates in the equation we get :
${{a}^{2}}{{({{t}_{1}}+{{t}_{2}})}^{2}}=4b(a{{t}_{1}}{{t}_{2}}+c)$ ………………………….(1)
Substituting $C$’s coordinates in the equation, we get :
${{a}^{2}}{{({{t}_{3}}+{{t}_{2}})}^{2}}=4b(a{{t}_{3}}{{t}_{2}}+c)$ ………………………….(2)
Comparing equations (1) and (2), we find that it can be interpreted like a quadratic in (let’s say $t$). We notice that ${{t}_{2}}$ remains the same in (1) and (2) while the value of $t$ keeps changing from ${{t}_{1}}$ to ${{t}_{3}}$. Therefore, we can say that ${{t}_{1}}$ and ${{t}_{3}}$ are the roots of the equation : ${{a}^{2}}{{(t+{{t}_{2}})}^{2}}=4b(at{{t}_{2}}+c)$ ……..(3)
Simplifying (3), we get :
$\begin{aligned} & {{a}^{2}}({{t}^{2}}+t_{2}^{2}+2t{{t}_{2}})=4b(at{{t}_{2}}+c) \\\ & \Rightarrow {{a}^{2}}{{t}^{2}}+2{{a}^{2}}t{{t}_{2}}+{{a}^{2}}{{t}_{2}}^{2}=4abt{{t}_{2}}+4bc \\\ & \Rightarrow {{a}^{2}}{{t}^{2}}+t(2{{a}^{2}}{{t}_{2}}-4ab{{t}_{2}})+({{a}^{2}}{{t}_{2}}^{2}-4bc)=0 \\\ \end{aligned}$
Now, it is more clearly visible why (3) was interpreted as a quadratic in $t$.
If ${{t}_{1}}$ and ${{t}_{3}}$ are the roots of the quadratic, then by general relations between the roots of a quadratic equation, we can say that :
$\begin{aligned} & {{t}_{1}}+{{t}_{3}}=\dfrac{4ab{{t}_{2}}-2{{a}^{2}}{{t}_{2}}}{{{a}^{2}}} \\\ & \Rightarrow {{t}_{1}}+{{t}_{3}}=\dfrac{4b{{t}_{2}}-2a{{t}_{2}}}{a} \\\ \end{aligned}$ ……………………………..(4)
And, ${{t}_{1}}{{t}_{3}}=\dfrac{{{a}^{2}}{{t}_{2}}^{2}-4bc}{{{a}^{2}}}$ ………………………………(5)
Now, we earlier established that the coordinates of $A$ = $(a{{t}_{1}}{{t}_{3}},a({{t}_{1}}+{{t}_{3}}))$
Here, we can make use of the relation between the roots.
Since we need to find the locus of $A$, let its coordinates be $(h,k)$.
Hence, we can say that :
$\begin{aligned} & h=a{{t}_{1}}{{t}_{3}} \\\ & \Rightarrow {{t}_{1}}{{t}_{3}}=\dfrac{h}{a} \\\ \end{aligned}$ and $\begin{aligned} & k=a({{t}_{1}}+{{t}_{3}}) \\\ & \Rightarrow {{t}_{1}}+{{t}_{3}}=\dfrac{k}{a} \\\ \end{aligned}$
Using the value we got from (5), we can say :
$\begin{aligned} & \dfrac{h}{a}=\dfrac{{{a}^{2}}{{t}_{2}}^{2}-4bc}{{{a}^{2}}} \\\ & \Rightarrow ah={{a}^{2}}{{t}_{2}}^{2}-4bc \\\ & \Rightarrow {{a}^{2}}{{t}_{2}}^{2}=ah+4bc \\\ & \Rightarrow t_{2}^{2}=\dfrac{ah+4bc}{{{a}^{2}}} \\\ \end{aligned}$ …………………………….(6)
Using the expression we got from (4), we can say :
$\begin{aligned} & \dfrac{k}{a}=\dfrac{4b{{t}_{2}}-2a{{t}_{2}}}{a} \\\ & \Rightarrow k={{t}_{2}}(4b-2a) \\\ & \Rightarrow {{t}_{2}}=\dfrac{k}{4b-2a} \\\ \end{aligned}$ …………………………(7)
Since, we got two values from (6) and squaring (7) and these are for a constant, these two values need to be equal. Hence, equating (6) and square of (7), we get :
$\begin{aligned} & \dfrac{ah+4bc}{{{a}^{2}}}=\dfrac{{{k}^{2}}}{{{(4b-2a)}^{2}}} \\\ & \Rightarrow (16{{b}^{2}}+4{{a}^{2}}-16ab)(ah+4bc)={{a}^{2}}{{k}^{2}} \\\ & \Rightarrow 16ah{{b}^{2}}+64{{b}^{3}}c+4{{a}^{3}}h+16{{a}^{2}}bc-16{{a}^{2}}bh-64a{{b}^{2}}c={{a}^{2}}{{k}^{2}} \\\ & \Rightarrow {{a}^{2}}{{k}^{2}}=h(16a{{b}^{2}}+4{{a}^{3}}-16{{a}^{2}}b)+64{{b}^{3}}c+16{{a}^{2}}bc-64a{{b}^{2}}c \\\ \end{aligned}$
To get the final locus, all we need to do is replace $(h,k)$ with $(x,y)$. Doing so, we get :
${{a}^{2}}{{y}^{2}}=x(16a{{b}^{2}}+4{{a}^{3}}-16{{a}^{2}}b)+64{{b}^{3}}c+16{{a}^{2}}bc-64a{{b}^{2}}c$
This equation represents a parabola, because here, the degree of $y$ is 2 but the degree of $x$ is 1, and there are no terms of $y$ or ${{x}^{2}}$ or $xy$ . Thus, this equation represents a parabola.
Hence proved, the locus of the third angular point will be a parabola.

Note: It might be difficult to understand how the triangle is placed. Here’s a diagram to ease out the process :

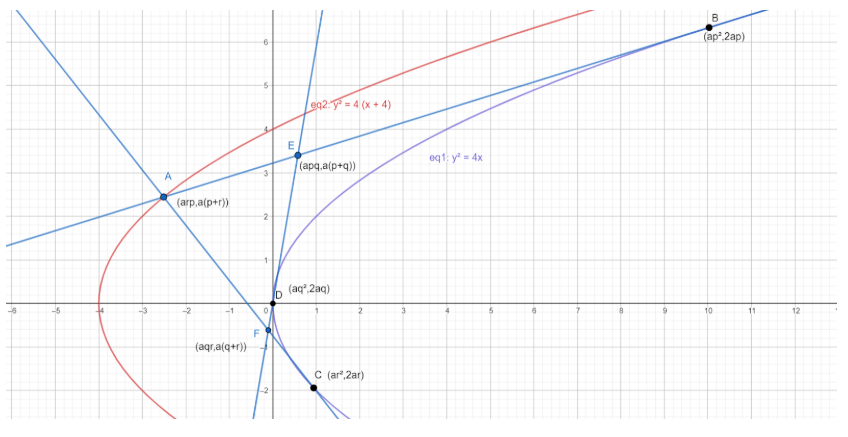
As you can see, the extended sides of the triangle act as tangents to the violet parabola, and the triangle $ABC$ is analogous to triangle $AEF$ in this figure.