Question
Question: The sides of a triangle inscribed in a given circle subtend angle \(\alpha ,\beta \) and \(\gamma \)...
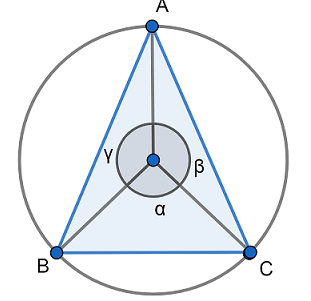
The sides of a triangle inscribed in a given circle subtend angle α,β and γ at the center. The minimum value of the arithmetic means of cos(α+2π),cos(β+2π) and cos(γ+2π) is equal to
A. 0
B. 21
C. −1
D. −23
Solution
To find the arithmetic means of cos(α+2π),cos(β+2π) and cos(γ+2π), we will add them and divide the sum by 3. We will use the property that the sum of angles subtended at the center of the circle is 360∘. Then by simplifying the obtained equations we will get the desired answer.
Complete step by step answer:
We have been given that the sides of a triangle inscribed in a given circle subtend angle α,β and γ at the center.
We have to find the minimum value of the arithmetic means of cos(α+2π),cos(β+2π) and cos(γ+2π).
Now, as seen in the figure the angles α,β and γ subtend at the center. We know that the sum of all angles subtended at the center of the circle is 360∘.
So we have α+β+γ=360∘
Now, the arithmetic mean will be given as
⇒3cos(α+2π)+cos(β+2π)+cos(γ+2π)
Now, we have to find the minimum value and the arithmetic mean has minimum value when
