Question

The sides of a triangle are three consecutive natural numbers and its largest angle is twice the smallest one, then the sides are
(a) 6, 7, 8
(b) 4, 5, 6
(c) 1, 2, 3
(d) 3, 4, 5

Answer 1

Hint: Assume the three sides of the triangle in terms of any variable with the difference ‘1’. Now use sine rule to find the length of sides. Sine rule is given as,
$\dfrac{\operatorname{sinA}}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}.$

Complete step-by-step answer:
Let us suppose the sides of the triangle as n, n+1, n+2 because it is given that sides are three consecutive natural numbers.
Now, it is given that the largest angle of the triangle is twice the smaller one.

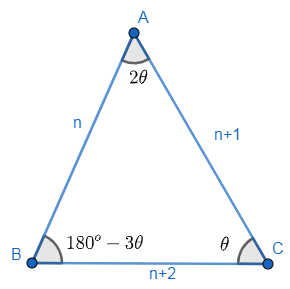
We know the property of a triangle that the opposite side of the larger angle is greater than the opposite side of the smaller angle.
So, the relation in sides is given as,
nHence, from triangle ABC in the diagram we will get
$\angle C<\angle B<\angle A$
Let $\angle C$ be $\theta$, hence $\angle A$ would be $2\theta$, as it is given in the question that the largest angle is twice the smallest one.
So, the angle B can be written as ${{180}^{o}}-3\theta$, by using the property of triangle i.e., sum of all interior triangle is ${{180}^{\circ }}$ always.
Now, we can apply sine Rule in $\Delta ABC$ which is given as,
$\dfrac{\sin A}{n+2}=\dfrac{\sin B}{n+1}=\dfrac{\sin C}{n}$
Substituting the corresponding values, we get
$\dfrac{\sin 2\theta }{n+2}=\dfrac{\sin \left( 180-3\theta \right)}{n+1}=\dfrac{\sin \theta }{n}..............\left( i \right)$
Now we can use identities of trigonometric which are given as
$\sin 2\theta =2\sin \theta \cos \theta$ and $\sin \left( 180-\theta \right)=\sin \theta$
Hence, equation (i) can be written as,
$\dfrac{2\sin \theta \cos \theta }{n+2}=\dfrac{\sin 3\theta }{n+1}=\dfrac{\sin \theta }{n}$
Now, use $\sin 3\theta =3\sin \theta -4si{{n}^{3}}\theta$ to further solve the above equation. Hence, we get
$\dfrac{2\sin \theta \cos \theta }{n+2}=\dfrac{3\sin \theta -4si{{n}^{3}}\theta }{n+1}=\dfrac{\sin \theta }{n}$
$\dfrac{2\sin \theta \cos \theta }{n+2}=\dfrac{\sin \theta \left( 3-4{{\sin }^{2}}\theta \right)}{n+1}=\dfrac{\sin \theta }{n}$
Now, we can divide the whole equation by $\sin \theta$ , and hence we get
$\dfrac{2\cos \theta }{n+2}=\dfrac{3-4{{\sin }^{2}}\theta }{n+1}=\dfrac{1}{n}..............\left( ii \right)$
Now, we can solve the equation (ii) by solving two equations individually, given as
$\begin{aligned} & \dfrac{2\cos \theta }{n+2}=\dfrac{1}{n}.................\left( iii \right) \\\ & \dfrac{3-4{{\sin }^{2}}\theta }{n+1}=\dfrac{1}{n}.................\left( iv \right) \\\ \end{aligned}$
Now, we can get value of $\cos \theta$ from equation (iii) as
$\cos \theta =\dfrac{1}{2}\left( \dfrac{n+2}{n} \right)................\left( v \right)$
We know ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, use this identity in equation (iv) to convert ‘sine’ function to ‘cosine’. Hence, we get
$\begin{aligned} & \dfrac{3-4(1-co{{s}^{2}}\theta )}{n+1}=\dfrac{1}{n} \\\ & \Rightarrow \dfrac{3-4+4co{{s}^{2}}\theta }{n+1}=\dfrac{1}{n} \\\ & \Rightarrow 4co{{s}^{2}}\theta -1=\dfrac{n+1}{n} \\\ & \Rightarrow 4co{{s}^{2}}\theta =\dfrac{n+1}{n}+1=\dfrac{n+1+n}{n}=\dfrac{2n+1}{n} \\\ & \Rightarrow co{{s}^{2}}\theta =\dfrac{1}{4}\left( \dfrac{2n+1}{n} \right)........(vi) \\\ \end{aligned}$
Now put the value of $\cos \theta$ from the equation (v) in the equation (vi) for getting the values of ‘n’, we get
${{\left( \left( \dfrac{1}{2} \right)\left( \dfrac{n+2}{n} \right) \right)}^{2}}=\dfrac{1}{4}\left( \dfrac{2n+1}{n} \right)$
$\left( \dfrac{1}{4}{{\left( \dfrac{n+2}{n} \right)}^{2}} \right)=\dfrac{1}{4}\left( \dfrac{2n+1}{n} \right)$
$\dfrac{{{\left( n+2 \right)}^{2}}}{n}=\dfrac{\left( 2n+1 \right)}{1}$
On cross multiplying the above equation, we get
${{\left( n+2 \right)}^{2}}=n\left( 2n+1 \right)$
On opening the bracket, we get
${{n}^{2}}+4n+4=2{{n}^{2}}+n$
$\Rightarrow {{n}^{2}}-3n-4=0$
Now, we can factorise the above equation by splitting the middle term, i.e., ‘-3’ to ‘-4’ and ‘1’. Hence, we get
$\begin{aligned} & {{n}^{2}}-4n+n-4=0 \\\ & \Rightarrow n\left( n-4 \right)+1\left( n-4 \right)=0 \\\ & \Rightarrow (n-4)(n+1)=0 \\\ \end{aligned}$
Hence,
n + 1 = 0 or n – 4 = 0
n = -1 or n = 4
As n = -1 is not possible. As a side of the triangle cannot be negative and ‘n’ is a natural number as well. So, n = 4.
Hence, sides of triangle can be given as n, n+1, n+2 i.e., 4, 5, 6
So, option (b) is the correct answer.

Note: One can apply cosine formula as well for solving the given question. As cosine formula is given as,
$\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Hence,
$\cos 2\theta =\dfrac{{{n}^{2}}+{{\left( n+1 \right)}^{2}}-{{\left( n+2 \right)}^{2}}}{2n\left( n+1 \right)}$ and $\cos \theta =\dfrac{{{\left( n+2 \right)}^{2}}+{{\left( n+1 \right)}^{2}}-{{n}^{2}}}{2\left( n+2 \right)\left( n+1 \right)}$
Now, solve the above equation to get ‘n’.
Calculation is the important part of the side as well. One may go wrong with the sine rule equation as well. Sine rule is given as
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}$
Here (a, b, c) sides are opposite to the angles A, B, C. So, be clear with the terms in the expression of sine rule.