Question

The sides of a triangle are in A.P. and its area is $\dfrac{3}{5}{\text{th}}$ of an equilateral triangle of the same perimeter. Prove that its sides are in the ratio $3:5:7$.

Answer 1

Take sides to be k +d, k, k –d. Then find the perimeter of the equilateral triangle by adding all the sides of the triangle. Then use formula of area of equilateral triangle which is given as-
Area of equilateral triangle = $\dfrac{{\sqrt 3 }}{4}{\left( x \right)^2}$ where x is the value of its side.
Then use Area of triangle=$\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$ where a , b, c are sides of triangle and s=$\dfrac{{a + b + c}}{2}$
Put the values and equate it to $\dfrac{3}{5}{\text{th}}$ of the area of the equilateral triangle of the same perimeter.

Complete step by step solution:
Given the sides of the triangle are in A.P. which means their common difference is the same. So we can take sides to be k +d, k, k –d.

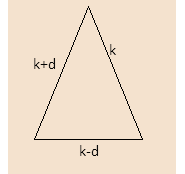
Now it is given that the area of triangle = $\dfrac{3}{5}{\text{th}}$ of an equilateral triangle of same perimeter--- (i)
We have to prove the sides are in ratio $3:5:7$.
Now we know that the sides of equilateral triangle are equal so let the side of equilateral triangle be k then perimeter of triangle is given as-
Perimeter=$k + k + k = 3k$
Now we know the area of equilateral triangle is given as-
Area of equilateral triangle = $\dfrac{{\sqrt 3 }}{4}{\left( x \right)^2}$ where x is the value of its side.
On putting the values in the formula we get,
Area of equilateral triangle=$\dfrac{{\sqrt 3 }}{4}{k^2}$
Now we know that area of triangle is given as,
Area of triangle=$\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$ where a , b, c are sides of triangle and s=$\dfrac{{a + b + c}}{2}$
So here s=$\dfrac{{k + d + k + k - d}}{2} = \dfrac{{3k}}{2}$
Now on substituting the given values in eq. (i) we get,
\Rightarrow \sqrt {\dfrac{{3k}}{2}\left( {\dfrac{{3k}}{2} - k + d} \right)\left( {\dfrac{{3k}}{2} - k} \right)\left( {\dfrac{{3k}}{2} - k - d} \right)} = \dfrac{3}{5} \times \left\\{ {\dfrac{{\sqrt 3 }}{4}{k^2}} \right\\}
On squaring both side we get,
\Rightarrow \dfrac{{3k}}{2}\left( {\dfrac{{3k}}{2} - k + d} \right)\left( {\dfrac{{3k}}{2} - k} \right)\left( {\dfrac{{3k}}{2} - k - d} \right) = \dfrac{9}{{25}} \times {\left\\{ {\dfrac{{\sqrt 3 }}{4}{k^2}} \right\\}^2}
On simplifying we get,
$\Rightarrow \dfrac{{3k}}{2}\left( {\dfrac{{3k - 2k + 2d}}{2}} \right)\left( {\dfrac{{3k - 2k}}{2}} \right)\left( {\dfrac{{3k - 2k - 2d}}{2}} \right) = \dfrac{9}{{25}} \times \dfrac{3}{{16}}{k^4}$
On cancelling the common term we get,
$\Rightarrow \left( {\dfrac{{k + 2d}}{2}} \right)\left( {\dfrac{k}{2}} \right)\left( {\dfrac{{k - 2d}}{2}} \right) = \dfrac{9}{{25}} \times \dfrac{1}{8}{k^3}$
We know that $\left( {a - b} \right)\left( {a + b} \right) = {a^2} - {b^2}$ so putting a=k and b=$2d$ , we get,
$\Rightarrow \left( {{k^2} - 4{d^2}} \right)\dfrac{k}{8} = \dfrac{9}{{25}} \times \dfrac{1}{8}{k^3}$
On again cancelling the common terms we get,
$\Rightarrow {k^2} - 4{d^2} = \dfrac{9}{{25}} \times {k^2}$
On taking the same terms together we get,
$\Rightarrow 4{d^2} = {k^2} - \dfrac{9}{{25}} \times {k^2}$
On solving we get,
$\Rightarrow 4{d^2} = \dfrac{{25{k^2} - 9{k^2}}}{{25}} = \dfrac{{16{k^2}}}{{25}}$
Then on solving we get,
$\Rightarrow \dfrac{d}{k} = \dfrac{{\sqrt 4 }}{{\sqrt {25} }} = \dfrac{2}{5}$
The sides of triangle are in ratio-
$\Rightarrow k - d: k: k + d$
On dividing the ratio by k we get,
$\Rightarrow 1 - \dfrac{d}{k}:1:1 + \dfrac{d}{k}$
On putting the values we get,
$\Rightarrow 1 - \dfrac{2}{5}:1:1 + \dfrac{2}{5} = \dfrac{{5 - 2}}{5}:1:\dfrac{{5 + 2}}{5}$
On solving we get,
$\Rightarrow \dfrac{3}{5}:1:\dfrac{7}{5}$
On multiplying the numbers by five we get,
$\Rightarrow 3:5:7$
Hence proved

Note:
Here the students can also assume the sides of the equilateral triangle to be a, b, and c where $a = b = c$ then the perimeter of the equilateral triangle = $a + a + a = 3a$. Now this equilateral triangle has the same perimeter as the triangle having sides in the A.P. series. Then Perimeter of the triangle=$k + k - d + k + d = 3k$
Then according to question, $3k = 3a \Rightarrow k = a$
So the value of the side we put in the area of the equilateral triangle will be k as given in the question.