Question
Question: The sides of a right angled triangle are in A.P. The ratio of sides is A.\[1:2:3\] B.\[2:3:4\] ...
The sides of a right angled triangle are in A.P. The ratio of sides is
A.1:2:3
B.2:3:4
C.3:4:5
D.5:8:3
Solution
Here, the sides of the triangle are in AP, so we will use the formula of n terms of ab AP to solve the question. We will assume the sides to be any variable. Then, we will apply Pythagoras Theorem in the right angled triangle and get the value of either of the two variables. Substituting the value of one variable and then, eliminating the other, we would find the required ratio of the sides.
Formulas Used:
We will use the following formulas:
1.(a+b)2=a2+b2+2ab
2.(a−b)2=a2+b2−2ab
3.The Pythagoras theorem, (AC)2=(AB)2+(BC)2, where AC is the hypotenuse of a right angled triangle.
Complete step-by-step answer:
The sides of a right angled triangle are in Arithmetic Progression (A.P.).
As we know, an arithmetic progression is a sequence in which the difference of any two consecutive terms is a constant.
Let us assume the sides of the right angled triangle be a−d, a, a+d. Here, a is the first term of the AP and d is the common difference.
Clearly, the largest side or the hypotenuse of the right angled triangle would be a+d.
Hence, applying Pythagoras Theorem in the right angled triangle, we get,
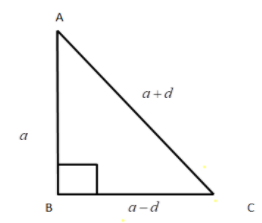
(AC)2=(AB)2+(BC)2
Now substituting the values of all sides in above equation, we get
⇒(a+d)2=(a)2+(a−d)2
Now, applying the formulas (a+b)2=a2+b2+2ab and (a−b)2=a2+b2−2ab to the above equation, we get
⇒a2+d2+2ad=a2+a2+d2−2ad
Solving further, we get
⇒a2−4ad=0
Now, taking a common, we get
⇒a(a−4d)=0
Hence, either a=0 or a−4d=0
Now, a=0 is not possible because a is one of the sides of the right angled triangle, hence it cannot be 0. Therefore,
⇒a−4d=0
Adding 4d on both sides, we get
⇒a=4d
Hence, the three sides of the right angled triangle are:
AB =a=4d
BC =a−d=4d−d=3d
AC =a+d=4d+d=5d
Hence, the sides a−d , a , a+d becomes 3d , 4d , 5di.e. they are in the ratio,3:4:5.
Hence, option C is the correct answer.
Note: We know that the first term of the AP is a and its common difference is d .
The formula of finding nth term of an AP is: a+(n−1)d
Hence, second and third terms of an AP, where n=2 and n=3 respectively, would be:
Second term =a+(2−1)d=a+d
And, third term =a+(3−1)d=a+2d
Now, when we are given that any three numbers are in AP, we do not follow the above rule of taking the first term as a and then taking the values of other terms depending upon it.
Else, for a meanwhile, we let the first term as a−d .
This will give us the value of other two terms as:
Second term =(a−d)+(2−1)d
Simplifying the terms, we get
⇒ Second term =a−d+d=a
And,
Third term=(a−d)+(3−1)d
Simplifying the terms, we get
⇒Third term =a−d+2d=a+d
Hence, whenever we have to let 3 sides of a triangle or any 3 numbers, we let them as:
a−d , a , a+d
As, whenever we would add these numbers, common difference, d would cancel out, leaving only one variable a and making the question easier.
