Question

The sides BC, CA and AB of a triangle ABC are of lengths a, b, c respectively. If D is the mid – point of BC and AD is perpendicular to AC, then the value of $\cos A\cos C$ is
(a) $\dfrac{3\left( {{a}^{2}}-{{c}^{2}} \right)}{2ac}$
(b) $\dfrac{2\left( {{a}^{2}}-{{c}^{2}} \right)}{3ac}$
(c) $\dfrac{\left( {{a}^{2}}-{{c}^{2}} \right)}{3ac}$
(d) $\dfrac{2\left( {{c}^{2}}-{{a}^{2}} \right)}{3ac}$

Answer 1

Hint: Draw the $\Delta ABC$, as mentioned. $AD\bot AC$ and D is mid – point of BC. i.e. BD = DC. Consider, $\Delta ADC$ formed find $\cos C$. Apply cosine law to the $\Delta ABC$ and find $\cos C$. Thus, form a relation connecting both $\cos C$. i.e. for ${{b}^{2}}$. Now, find $\cos A$ using the cosine formula, find $\cos A\cos C$ and simplify it.

Complete step-by-step answer:
Consider the $\Delta ABC$. D is the mid – point of the side BC. Now AD is the perpendicular to AC. i.e. $AD\bot AC$.

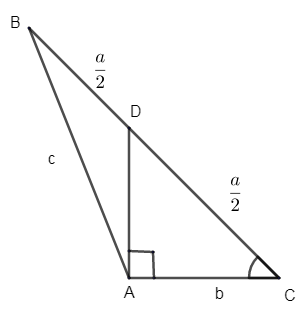
Let us first consider the right angled triangle DAC.
Let us consider C as the angle.
$\therefore \cos C$ = adjacent side / hypotenuse $=\dfrac{AC}{DC}$ [from the figure]
i.e. $\cos C=\dfrac{b}{\dfrac{a}{2}}=\dfrac{2a}{b}$
$\therefore \cos C=\dfrac{2a}{b} \to (1)$
Now, cosine rule of triangle states that the square of the length of any side of a triangle equals the sum of the squares of the length of the other sides minus twice their product multiplied by the cosine of their included angle. Hence, by cosine rule we can write,
${{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos C$
i.e. $2ab\cos C={{a}^{2}}+{{b}^{2}}-{{c}^{2}}$
$\therefore \cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} \to (2)$
Let us equate (1) and (2).
$\dfrac{2a}{b}=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$
$\dfrac{4a{{b}^{2}}}{a}={{a}^{2}}+{{b}^{2}}-{{c}^{2}}$, Simplify the expression,

& 4{{b}^{2}}={{a}^{2}}+{{b}^{2}}-{{c}^{2}} \\\ & \left( 4-1 \right){{b}^{2}}={{a}^{2}}-{{c}^{2}} \\\ & {{b}^{2}}=\dfrac{{{a}^{2}}-{{c}^{2}}}{3} \to (3) \\\ \end{aligned}$$ Similarly, from cosine formula, we can write, $$\begin{aligned} & {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2ab\cos A \\\ & 2cb\cos A={{b}^{2}}+{{c}^{2}}-{{a}^{2}} \\\ & \cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \to (4) \\\ \end{aligned}$$ Hence, $$\cos A.\cos C=\left( \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \right)\left( \dfrac{2b}{a} \right)$$ Put the value of $${{b}^{2}}$$ from equation (3). $$\therefore \cos A.\cos C=\left( \dfrac{{{a}^{2}}-{{c}^{2}}}{3}+{{c}^{2}}-{{a}^{2}} \right)\times \left( \dfrac{2b}{2bc\times a} \right)$$ $$\begin{aligned} & \cos A.\cos C=\left( \dfrac{{{a}^{2}}-{{c}^{2}}+3{{c}^{2}}-3{{a}^{2}}}{3} \right)\times \left( \dfrac{1}{ca} \right) \\\ & \cos A.\cos C=\dfrac{2{{c}^{2}}+2{{a}^{2}}}{3}\times \dfrac{1}{{{a}^{2}}}=\dfrac{2}{3}\left( \dfrac{{{c}^{2}}-{{a}^{2}}}{ca} \right) \\\ \end{aligned}$$ Hence, we got the value of $$\cos A.\cos C=\dfrac{2}{3}\left( \dfrac{{{c}^{2}}-{{a}^{2}}}{ca} \right)$$. $$\therefore $$ Option (d) is the correct answer. Note: Cosine law is useful for solving the missing information in a triangle. If all 3 sides of the triangle are known, the cosine rule allows one to find any angle measure. Similarly, if 2 sides and the angle between them are known, the cosine rule allows to find the $${{3}^{rd}}$$ side length.