Question

The sides AC and AB of $\Delta ABC$ touch the conjugate hyperbola of the hyperbola
$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ . If the vertex A lies on the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , then the side BC must touch:
(A) parabola
(B) circle
(C) hyperbola
(D) ellipse

Answer 1

Hint: Take the coordinate of the point A as $\left( a\cos \theta ,b\sin \theta \right)$ . The equation of the conjugate hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$ . Since the sides AB and AC are touching the conjugate hyperbola so, the side BC is the chord of contact with respect to point A. Equation of chord of contact is given by, $\dfrac{x{{x}_{1}}}{{{a}^{2}}}-\dfrac{y{{y}_{1}}}{{{b}^{2}}}=-1$ . Using this get the equation of the side BC by putting the coordinates $\left( a\cos \theta ,b\sin \theta \right)$ in the equation $\dfrac{x{{x}_{1}}}{{{a}^{2}}}-\dfrac{y{{y}_{1}}}{{{b}^{2}}}=-1$ . The equation of tangent on ellipse is given by $\dfrac{x{{x}_{1}}}{{{a}^{2}}}-\dfrac{y{{y}_{1}}}{{{b}^{2}}}=-1$ , where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point on the ellipse at which the tangent is drawn.

Complete step by step solution:

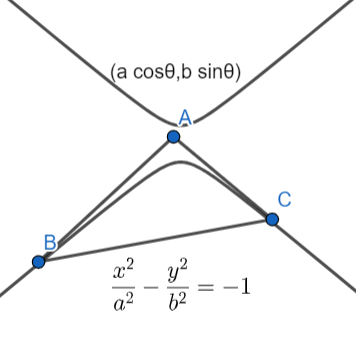
According to the question, it is given that the sides AC and AB of $\Delta ABC$ touch the conjugate hyperbola of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and the vertex A lies on the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ .
Since the vertex A lies on the ellipse so, let us assume the parametric form of coordinates for the point A.
In an ellipse which has equation, $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , the coordinate of a point in parametric form is given by $\left( a\cos \theta ,b\sin \theta \right)$ ………………..(1)
So, the coordinates of the point A is $\left( a\cos \theta ,b\sin \theta \right)$ .
$A\left( a\cos \theta ,b\sin \theta \right)$ …………………(2)
It is also given that the sides AB and AC are touching the conjugate of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ .
We need the equation of conjugate hyperbola of the hyperbola, $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ ……………………(3)
We can get the equation of the conjugate hyperbola after replacing 1 by -1 in equation (3).
Here, we have got the equation of the conjugate hyperbola, $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$ …………………….(4)
We know the equation of chord of contact of the conjugate hyperbola, $\dfrac{x{{x}_{1}}}{{{a}^{2}}}-\dfrac{y{{y}_{1}}}{{{b}^{2}}}=-1$ …………(5)
Here, $\left( {{x}_{1}},{{y}_{1}} \right)$ is the coordinate of the point with respect to which the chord of contact is drawn.
Since the sides AB and AC are touching the conjugate hyperbola so, the side BC is chord of contact with respect to point A.
So, $\left( {{x}_{1}},{{y}_{1}} \right)=\left( a\cos \theta ,b\sin \theta \right)$ ……………….(6)
Now, replacing ${{x}_{1}}$ by $a\cos \theta$ and ${{y}_{1}}$ by $a\sin \theta$ in equation (5), we get the equation of BC,

& \dfrac{x{{x}_{1}}}{{{a}^{2}}}-\dfrac{y{{y}_{1}}}{{{b}^{2}}}=-1 \\\ & \Rightarrow \dfrac{x\left( a\cos \theta \right)}{{{a}^{2}}}-\dfrac{y\left( b\sin \theta \right)}{{{b}^{2}}}=-1 \\\ \end{aligned}$$ $$\Rightarrow -\dfrac{x\cos \theta }{a}+\dfrac{y\sin \theta }{b}=1$$ $$\Rightarrow \dfrac{x\left( -\cos \theta \right)}{a}+\dfrac{y\sin \theta }{b}=1$$ ………………………….(7) We know that, $$\cos \left( \pi -\theta \right)=-\cos \theta $$ ……………..(8) $$sin\left( \pi -\theta \right)=sin\theta $$ ……………….(9) Now, using equation (7), equation (8), and equation (9), we get $$\begin{aligned} & \Rightarrow \dfrac{x\left( -\cos \theta \right)}{a}+\dfrac{y\sin \theta }{b}=1 \\\ & \Rightarrow \dfrac{x\cos \left( \pi -\theta \right)}{a}+\dfrac{y\sin \left( \pi -\theta \right)}{b}=1 \\\ \end{aligned}$$ $$\Rightarrow \dfrac{x\left( a\cos \left( \pi -\theta \right) \right)}{{{a}^{2}}}+\dfrac{y\left( b\sin \left( \pi -\theta \right) \right)}{{{b}^{2}}}=1$$ …………………………..(10) From equation, we have that in an ellipse which has equation $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ , the coordinate of a point in parametric form is given by $$\left( a\cos \theta ,b\sin \theta \right)$$ . The equation of the tangent at the point $$\left( a\cos \left( \pi -\theta \right),b\sin \left( \pi -\theta \right) \right)$$ on ellipse is $$\Rightarrow \dfrac{x\left( a\cos \left( \pi -\theta \right) \right)}{{{a}^{2}}}+\dfrac{y\left( b\sin \left( \pi -\theta \right) \right)}{{{b}^{2}}}=1$$ …………………(11) In equation (10) we have the equation of BC and in equation (11), we have the equation of the tangent. The equation (10) and equation (11) are equal. Therefore, BC touches the ellipse $$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ at the point $$\left( a\cos \left( \pi -\theta \right),b\sin \left( \pi -\theta \right) \right)$$ . Hence, the correct option is (D). Note: In this question, one might try to solve this question by assuming the coordinate of point A as $$\left( {{x}_{1}},{{y}_{1}} \right)$$ . If we do so, then our complexity will increase. To reduce the complexity, try to solve the question using parametric form of coordinates. One can take the equation of the conjugate hyperbola of the hyperbola $$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ as $$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$$ . This is wrong. The correct equation of the conjugate of the hyperbola will be $$\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=-1$$ .