Question

The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

• A. 20
• B. 25
• C. 40
• D. 30

Answer 1

Answer: (D)

30

Answer 2

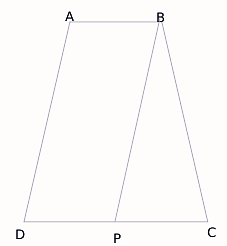
Let $DP =x$
$∴ AB =x$
Now $DP=CP$
So, $CD = 2x$
Now, if we denote the height of the trapezium as $h$,
Then, the area of parallelogram ABPD$$= xh
And Area of $△BPC=\frac{1}{2}xh$
Now, based on the given condition,
$xh-\frac{1}{2}xh=10$
$\frac{xh}{2}=10$
$⇒ xh=20$
Then, the area of trapezium $\frac{1}{2}(x+2x)h$
$=\frac{3}{2}xh$

$=\frac{3}{2} \times 10$
$=30$

So, the correct option is (D): $30$