Question

The shunt resistance required to allow $4\%$ of the main current through the galvanometer of resistance $48\Omega$ is:
a. $1\Omega$
b. $2\Omega$
c. $3\Omega$
d. $4\Omega$
e. $5\Omega$

Answer 1

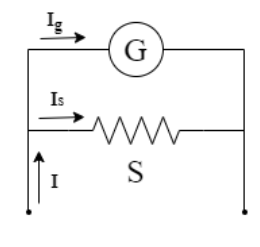
Shunt resistance is always connected in parallel connection to the galvanometer. Use the condition for parallel connection to get the required value.

Formula Used:
Ohm’s law:
$V = I.R$
Where,
V is voltage across the resistor,
I is current through the resistor,
R is the value of the resistance.

Complete answer:
Given:
Current through the galvanometer is $4\%$of main current, i.e. ${i_g} = \dfrac{{4i}}{{100}} = \dfrac{i}{{25}}$, where i is current through main circuit.
Resistance of the galvanometer is $G = 48\Omega$.

To find: The shunt resistance S(say).

Step 1:
Since, the shunt is connected parallel to the galvanometer hence the voltage drop across them will be the same. Also, the main current will get divided to pass through the galvanometer and the shunt. So, the current through the shunt will be ${i_s} = i - {i_g}$. Now, use ohm’s law both across the galvanometer and the shunt to get the relation:
${i_g}.G = {i_s}.S \\\ \Rightarrow S = \dfrac{{{i_g}.G}}{{{i_s}}} \\\$

Step 2:
Now, substitute the values of ${i_g}$, ${i_s}$and G to get:
$S = \dfrac{{{i_g}.G}}{{{i_s}}} \\\ = \dfrac{{\tfrac{i}{{25}}}}{{\left( {1 - \tfrac{i}{{25}}} \right)}} \times 48 = \dfrac{i}{{25}} \times \dfrac{{25}}{{24i}} \times 48 = 2\Omega \\\$

Hence, Required shunt resistance is (b) $2\Omega$..

Note: A galvanometer is shunted with a small resistance to make it an ammeter. It makes the effective resistance of the ammeter very low. Since, galvanometer is a very sensitive instrument, it can’t measure a large current. Using a low resistance shunt makes the current through the galvanometer very less.