Question

The shortest distance of (a, b, c) from x- axis is,
A. $\sqrt{{{a}^{2}}+{{b}^{2}}}$
B. $\sqrt{{{b}^{2}}+{{c}^{2}}}$
C. $\sqrt{{{c}^{2}}+{{a}^{2}}}$
D. $\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}$

Answer 1

Hint: We will be using the concepts 3-D geometry to solve the problem. We will first draw a figure which depicts the situation clearly then we will find the point which is perpendicular from the given point on the x-axis and we will then use the distance formula of the coordinate geometry to find the final answer.

Complete step-by-step answer:
Now, we have been given a point (a, b, c) and we have to find its shortest distance from x – axis. Now, firstly we will make a diagram to understand the problem.

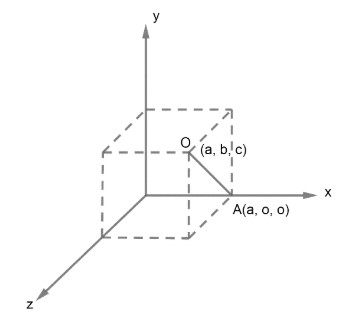
Now, we have to find the shortest distance of the point from the x – axis and we know the shortest distance is the perpendicular distance. So, we have to find the distance OA as shown in the diagram.
Now, we know the coordinates of O (a, b, c) and A (a, 0, 0). So, we will be using the formula of finding the distance between two points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ in 3-D is,
$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}+{{\left( {{z}_{1}}-{{z}_{2}} \right)}^{2}}}$
So, the distance between points (a, b, c) and (a, 0, 0) is
$\begin{aligned} & =\sqrt{{{\left( a-a \right)}^{2}}+{{\left( b-0 \right)}^{2}}+{{\left( c-0 \right)}^{2}}} \\\ & =\sqrt{{{0}^{2}}+{{b}^{2}}+{{c}^{2}}} \\\ & =\sqrt{{{b}^{2}}+{{c}^{2}}} \\\ \end{aligned}$
Therefore, the correct option is (B).

Note: To solve these types of questions it is important to visualize the situation by drawing a suitable diagram then one must apply the formula to find the required answer also it is important to note that we have used the distance formula to find the distance between two points the formula in 2-D is also similar to 3-D except the fact that we put z=0 in 2-D.