Question

The shortest distance from the line $3x\text{ + 4y = 25}$ to the circle ${{x}^{2}}\text{ + }{{\text{y}}^{2}}\text{ = 6x - 8y}$ is equal to

& A.\dfrac{1}{2} \\\ & B.\dfrac{7}{5} \\\ & C.\dfrac{11}{5} \\\ & D.\dfrac{1}{3} \\\ \end{aligned}$$

Answer 1

As we know the equation of circle so transform it into ${{\left( x\text{ - }{{\text{x}}_{1}} \right)}^{2}}\text{ + }{{\left( y\text{ - }{{\text{y}}_{1}} \right)}^{2}}\text{ = }{{\text{r}}^{2}}$ where $\left( {{x}_{1,}}\text{ }{{\text{y}}_{1}} \right)$ center’s point and r is radius. Then to find shortest distance, first find distance between center of circle and the given line using formula
\dfrac{\left| Aa+Bb+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$$$$$$ Where equation of line is \text{Ax+By+C}=0$$ and point is (a, b) and then subtract it with the given radius r.

Complete step-by-step solution:
In the question, equation of a line $3x\text{ + 4y = 25}$ and the circle ${{x}^{2}}\text{ + }{{\text{y}}^{2}}\text{ = 6x - 8y}$ is given and we have to find shortest distance between them.
So we can represent it by the diagram,
Let AB be the shortest distance between line and circle. Let O be the center of the circle so OA can be represented as the radius of the circle.
So we can represent it by the diagram,

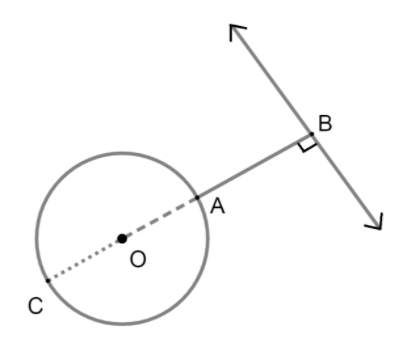
The circle and line represented in the diagram have equations $3x\text{ + 4y = 25}$ and ${{x}^{2}}\text{ + }{{\text{y}}^{2}}\text{ = 6x - 8y}$ respectively.
The given equation of circle is,
${{x}^{2}}\text{ + }{{\text{y}}^{2}}\text{ = 6x - 8y}$
Which we can write it as,
${{x}^{2}}\text{ + }{{\text{y}}^{2}}\text{ - 6x + 8y = 0}$
Now we will transform it into the form ${{\left( x\text{ - }{{\text{x}}_{1}} \right)}^{2}}\text{ + }{{\left( y\text{ - }{{\text{y}}_{1}} \right)}^{2}}\text{ = }{{\text{r}}^{2}}$ where $\left( {{x}_{1,}}\text{ }{{\text{y}}_{1}} \right)$ point of center and r is is radius. Here we add and subtract the square of half of the coefficient of x and y.
So we can write the equation of circles,

& {{x}^{2}}\text{ - 6x + 9 +}{{\text{y}}^{2}}\text{ + 8y + 16 = 16 + 9} \\\ & \Rightarrow {{\left( x\text{ - 3} \right)}^{2}}\text{ + }{{\left( y\text{ + 4} \right)}^{2}}\text{ = 25} \\\ \end{aligned}$$ Here the center of the circle is (3, -4) and radius is 5. The length of AB can be determined by subtracting the length of the radius from the length of OB. So we can say that, AB is equal to $$\left( \text{OB} -\text{OA} \right)$$ As the circle’s center is (3, -4) and the radius is 5. So the distance between the center of the circle and the line can be determined by using the formula, $$\dfrac{\left| Aa+Bb+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$$ Where the equation of line is $$\text{Ax }+\text{ By }+\text{ C }=\text{ }0$$ and point is (a, b). Here the equation is $$3x\text{ + 4y = 25}$$ which can also be written as $$3x\text{ + 4y - 25 = 0}$$ and point is (3, -4) so its distance will be, $$\begin{aligned} & \dfrac{\left| 3\times 3+4\left( -4 \right)-25 \right|}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \\\ & \Rightarrow \dfrac{\left| 9-16-25 \right|}{\sqrt{25}} \\\ \end{aligned}$$ Hence on simplification we get that length between point and circle is $$\dfrac{32}{5}$$ Hence the length of OB is $$\dfrac{32}{5}$$ The radius of given circle is 5. So the length AB is length of OB – length of radius. So the length is $$\dfrac{32}{5}\text{ - 5}\Rightarrow \dfrac{32\text{ - 25}}{5}\Rightarrow \dfrac{7}{5}$$ **Hence the correct option is ‘B’.** **Note:** If the equation of circle is given in form of $${{x}^{2}}\text{+}{{\text{y}}^{2}}+2gx+2fy+c=0$$ then, one should add and subtract some constants to make it appear in the form $${{\left( x\text{ - }{{\text{x}}_{1}} \right)}^{2}}\text{ + }{{\left( y\text{ - }{{\text{y}}_{1}} \right)}^{2}}\text{ = }{{\text{r}}^{2}}$$ where, center is $\left( {{x}_{1,}}\text{ }{{\text{y}}_{1}} \right)$ and r is radius. Also, if the distance between a point and line is said as shortest then, it represents the length of the perpendicular between point and line.