Solveeit Logo
Login

Question

Question: The shortest distance between the lines $\bar r = (1 - t)\hat i + (t - 2)\hat j + (3 - 2t)\hat k$ an...

The shortest distance between the lines rˉ=(1−t)i^+(t−2)j^+(3−2t)k^\bar r = (1 - t)\hat i + (t - 2)\hat j + (3 - 2t)\hat k and rˉ=(p+1)i^+(2p−1)j^+(2p+1)k^\bar r = (p + 1)\hat i + (2p - 1)\hat j + (2p + 1)\hat k is

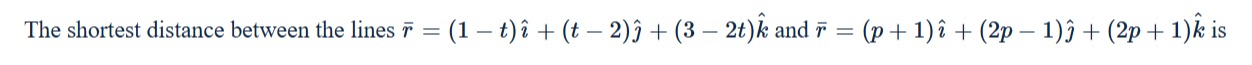
Answer

25\displaystyle \frac{2}{\sqrt{5}}

Explanation

Solution

Extract position and direction vectors from both lines. Compute a₂ – a₁ = (0, 1, –2) and b₁ × b₂ = (6, 0, –3) with |b₁ × b₂| = 3√5. The dot product (a₂ – a₁)·(b₁ × b₂) = 6. Then, d = 6/(3√5) = 2/√5.