Question

The shortest distance between the line $y=x$ and the curve ${{y}^{2}}=x-2$ is
A. $\dfrac{7}{4\sqrt{2}}$
B. $\dfrac{7}{8}$
C. $\dfrac{11}{4\sqrt{2}}$
D. $2$

Answer 1

In this question, we have to use the concept of normal lines of curves. We know that the shortest distance between two curves is along their common normal. So, we use both curve’s and the normal equations and get a point on parabola and then using the perpendicular distance formula get the shortest distance. 1. For a parabola, ${{\left( y-{{b}_{1}} \right)}^{2}}=4a\left( x-{{a}_{1}} \right)$ and point $p\left( {{x}_{1}},{{y}_{1}} \right)$ is on the curve, so equation of normal would be, $\left( y-{{b}_{1}}-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{a}_{1}}-{{x}_{1}} \right)$. 2.For a line, $y=mx+c$, so equation of normal is, $y=\dfrac{-1}{m}x+k$. 3. The condition for perpendicular lines having slope ${{m}_{1}}$and ${{m}_{2}}$ is given by, ${{m}_{1}}\times {{m}_{1}}=-1$, so for normal to parabola, we take slope as ${{m}_{Nr}}$ and for line as $m$and we have, $m\times {{m}_{Nr}}=-1\Rightarrow {{m}_{Nr}}=\dfrac{-1}{m}$. 4. For minimum distance between point $\left( {{x}_{1}},{{y}_{1}} \right)$ and line $ax+by+c=0$, $d=\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$.

Complete step by step answer:
We have been given a curve and a line in the question, so let us write it as below,
Curve 1 as $y=x$, line and curve 2 as ${{y}^{2}}=x-2$, parabola. We can draw these two as below,

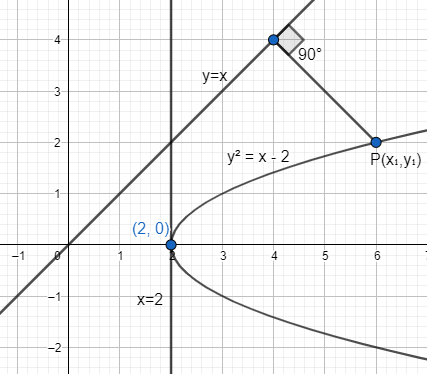
As we know that the shortest distance between two curve is measured along their common normal, so let us assume the common normal line is passing through point $p\left( {{x}_{1}},{{y}_{1}} \right)$ on curve parabola, ${{y}^{2}}=x-2$ and perpendicular to $y=x$. So, for curve 1, $y=x\Rightarrow m=1$, slope of normal = -1. The normal line’s equation is,
$y=-x+c\ldots \ldots \ldots \left( i \right)$
For parabola, ${{y}^{2}}=4a\left( x-p \right)$, the equation of normal passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is given as,
$\left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-p-{{x}_{1}} \right)$
Similarly, we have, ${{y}^{2}}=x-2$, $p=2,a=\dfrac{1}{4}$. So, we get the equation of the normal as,
$\begin{aligned} & \left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2\times \dfrac{1}{4}}\left( x-2-{{x}_{1}} \right) \\\ & \Rightarrow \left( y-{{y}_{1}} \right)=-2{{y}_{1}}\left( x-{{x}_{1}} \right)+4{{y}_{1}} \\\ & \Rightarrow y=-2{{y}_{1}}x+2{{y}_{1}}{{x}_{1}}+4{{y}_{1}}+{{y}_{1}} \\\ & \Rightarrow y=-2{{y}_{1}}x+5{{y}_{1}}+2{{y}_{1}}{{x}_{1}}\ldots \ldots \ldots \left( ii \right) \\\ \end{aligned}$
We can see that equation (i) an (ii) are the same equations, that is,
$\begin{aligned} & y=-x+c \\\ & y=-2{{y}_{1}}x+5{{y}_{1}}+2{{y}_{1}}{{x}_{1}} \\\ \end{aligned}$
So, by comparing both the equations, we get,
$\begin{aligned} & -1=-2{{y}_{1}}\Rightarrow {{y}_{1}}=\dfrac{1}{2} \\\ & c=5{{y}_{1}}+2{{y}_{1}}{{x}_{1}}\Rightarrow c=\dfrac{5}{2}+{{x}_{1}} \\\ \end{aligned}$
We know that $p\left( {{x}_{1}},{{y}_{1}} \right)$ satisfies the curve parabola, ${{y}^{2}}=x-2$ also, so we have,
${{y}_{1}}^{2}={{x}_{1}}-2$
We know that ${{y}_{1}}=\dfrac{1}{2}$, so substituting that value, we get,
$\begin{aligned} & \Rightarrow {{\left( \dfrac{1}{2} \right)}^{2}}={{x}_{1}}-2 \\\ & \Rightarrow {{x}_{1}}=2+\dfrac{1}{4} \\\ & \Rightarrow {{x}_{1}}=\dfrac{9}{4} \\\ \end{aligned}$
So, we get the point P as $\left( \dfrac{9}{4},\dfrac{1}{2} \right)$. So, the shortest distance between curves is the perpendicular distance between point P and line y=x. Now rearranging it we have x-y=0. Comparing it with equations of line $ax+by+c=0$ we have a=1, b=-1 and c=0. So, we will use formula for the perpendicular distance d between point $\left( {{x}_{1}},{{y}_{1}} \right)$ and line $ax+by+c=0$ and substitute the values as given below,
$\begin{aligned} & d=\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right| \\\ & \Rightarrow d=\left| \dfrac{{{y}_{1}}-{{x}_{1}}}{\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 1 \right)}^{2}}}} \right| \\\ & \Rightarrow d=\left| \dfrac{\dfrac{1}{2}-\dfrac{9}{4}}{\sqrt{2}} \right| \\\ & \Rightarrow d=\dfrac{7}{4\sqrt{2}} \\\ \end{aligned}$
So, the correct answer is “Option A”.

Note: In this question, students make mistakes in the equation of normal like, they take the slope of the tangent instead of normal, so this should be kept in mind. In the equation of the normal, for parabola, we have to take $\left( y-{{b}_{1}}-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{a}_{1}}-{{x}_{1}} \right)$ and not $\left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right)$.