Question

The shortest distance between the following pair of lines: $\vec{r} = \hat{i} + 2\hat{j} - 4\hat{k} + \lambda(2\hat{i} + 3\hat{j} + 6\hat{k})$ and $\vec{r} = 3\hat{i} + 3\hat{j} - 5\hat{k} + \mu(2\hat{i} + 3\hat{j} + 6\hat{k})$ is $\frac{\sqrt{293}}{K}$.

Find the value of $K$.

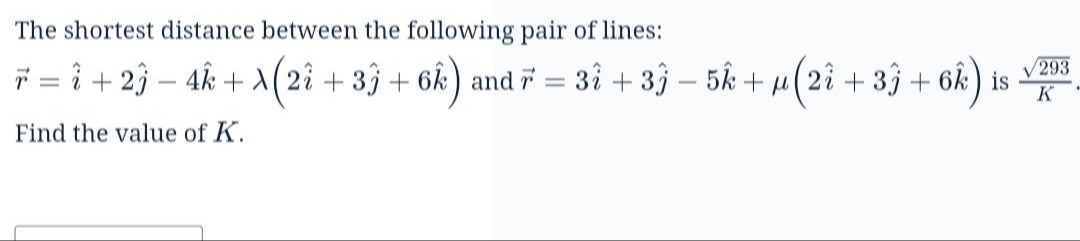
Answer 1

7

Answer 2

Solution:

1. Identify Points and Direction Vector:
   Line 1 passes through $A(1,2,-4)$ with direction vector $\vec{d} = (2,3,6)$.
   Line 2 passes through $B(3,3,-5)$ with the same direction vector $\vec{d} = (2,3,6)$.

2. Find Vector Connecting the Two Points:
   $\vec{AB} = B - A = (3-1,\; 3-2,\; -5-(-4)) = (2,\,1,\,-1)$.

3. Compute the Cross Product $\vec{AB} \times \vec{d}$:

   $$\vec{AB} \times \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & -1 \\ 2 & 3 & 6 \\ \end{vmatrix} = \hat{i}(1\cdot6 - (-1)\cdot3) - \hat{j}(2\cdot6 - (-1)\cdot2) + \hat{k}(2\cdot3-1\cdot2)$$ $$= \hat{i}(6+3) - \hat{j}(12+2) + \hat{k}(6-2) = (9,\,-14,\,4).$$

4. Calculate the Magnitudes:

   $$|\vec{AB} \times \vec{d}| = \sqrt{9^2 + (-14)^2 + 4^2} = \sqrt{81 + 196 + 16} = \sqrt{293}.$$ $$|\vec{d}| = \sqrt{2^2+3^2+6^2} = \sqrt{4+9+36} = \sqrt{49} = 7.$$

5. Determine the Shortest Distance:

   $$\text{Distance} = \frac{|\vec{AB} \times \vec{d}|}{|\vec{d}|} = \frac{\sqrt{293}}{7}.$$

   This is given as $\frac{\sqrt{293}}{K}$, which implies $K = 7$.