Question
Question: The shape of an ancient water clock jug is such that water level descends at a constant rate at all ...
The shape of an ancient water clock jug is such that water level descends at a constant rate at all times. If the water level falls by 4cm every hour, determine the shape of the jar, i.e., specify x as a function of y . The radius of the drain hole is 2mm and can be assumed to be very small compared to x .
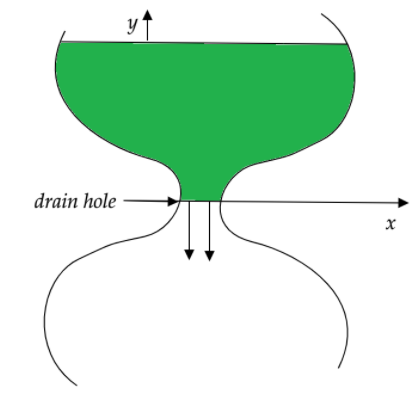
Solution
If the water in the jug is at a certain height, it will cause the water to flow through the hole with a certain velocity and as a result, the height will decrease at a certain rate. The volume of water flowing out through the orifice will be proportional to the decrease in height of water in the jug. We will make use of this property to find our answer.
Formula Used: vy=2gy , V=vy×A
Complete step by step solution:
Let the height of the water column in the jug at a certain instant of time, say t=0 , is y
The velocity of the water through the drain hole will be 2gy
Radius of the drain hole (r)=2mm=2×10−3m[∵1mm=10−3m]
Hence area of the drain hole (A)=πr2
Substituting the values, we get
