Question

The shadow of a tower standing on level ground is found to be 40 m longer when the Sun’s altitude is ${{30}^{\circ }}$ than when it was ${{60}^{\circ }}.$ Find the height of the tower. $\left( \text{Given }\sqrt{3}=1.732 \right)$

Answer 1

To solve the given question, we will assume that the height of the tower is h. Then, we will assume that when the sun’s altitude is ${{30}^{\circ }},$ the length of the shadow of the building is x and when the sun’s altitude is ${{60}^{\circ }},$ the length of the shadow of the building on the ground is y. Then, we will develop a relation between x and y using the information given in the question that the difference in x and y is 40 m. Now, we will apply trigonometry in the triangle formed by the length of the shadow when the sun's altitude is ${{30}^{\circ }}$ and the height of the building as h.

Complete step-by-step answer:
To start with, we are going to first draw a rough sketch. In this, we are considering the length of the shadow on level ground as x when the sun’s altitude is ${{30}^{\circ }}$ and the length of shadow as y when the sun’s altitude is ${{60}^{\circ }}.$ The height of the tower is h.

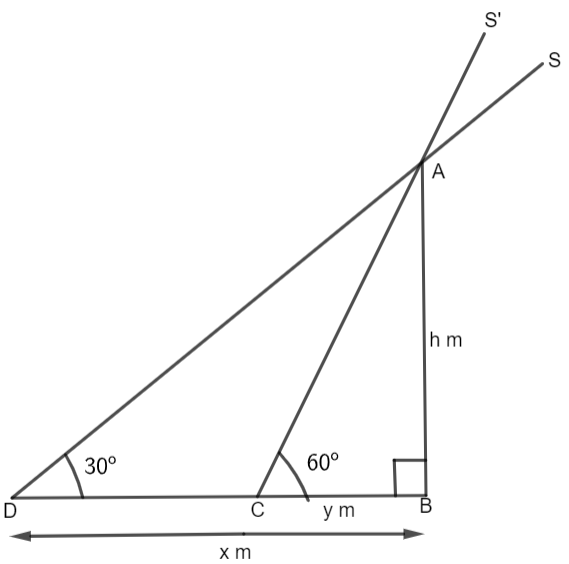
In the figure, BC and BD are the lengths of the shadows when the sun’s altitude is ${{60}^{\circ }}$ and ${{30}^{\circ }}$ respectively. AB is the height of the building. S and S’ are positions of the sun. Now, it is given in the question that the difference in length of shadows is 40m. Thus, we will get,
$x-y=40m.....\left( i \right)$
Now, we will consider the right-angled triangle ABD. We know that in any right-angled triangle the ratio of the perpendicular to the base is given by tan of the angle between the hypotenuse and the base. Thus, we can say that,
$\tan D=\dfrac{AB}{BD}$
$\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{x}$
Now, the value of $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}.$ So, we have,
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{x}$
$\Rightarrow x=h\sqrt{3}.....\left( ii \right)$
Now, we will consider the right-angled triangle ABC. In this triangle, BC is the base and AB is the perpendicular. So, we have,
$\tan C=\dfrac{AB}{BC}$
$\Rightarrow \tan {{60}^{\circ }}=\dfrac{h}{y}$
Now, the value of $\tan {{60}^{\circ }}=\sqrt{3}.$ So, we have,
$\Rightarrow \sqrt{3}=\dfrac{h}{y}$
$\Rightarrow y=\dfrac{h}{\sqrt{3}}.....\left( iii \right)$
Now, we will put the values of x and y from (ii) and (iii) to (i). Thus, we will get,
$\Rightarrow h\sqrt{3}-\dfrac{h}{\sqrt{3}}=40m$
$\Rightarrow \dfrac{\sqrt{3}\left( h\sqrt{3} \right)-h}{\sqrt{3}}=40m$
$\Rightarrow \dfrac{3h-h}{\sqrt{3}}=40m$
$\Rightarrow \dfrac{2h}{\sqrt{3}}=40m$
$\Rightarrow h=20\sqrt{3}m$
$\Rightarrow h=20\times 1.732=34.64m$
Thus, the height of the building is 34.64 m.

Note: While solving the question, we have assumed that the building is perfectly perpendicular to the ground level. Also, we have assumed the building as a straight line and not as a 3D object because in 3D, the shadow of each dimension of the building would be different and we are not given this much information to solve the question by considering 3 dimensions of the building.