Question

The shadow of a tower standing on a level ground is found to be 60 metres longer
when the sun's altitude is ${30^0}$ than when it is ${45^0}$. Find the height of the tower.

Answer 1

Hint:- Draw figure and then use trigonometry identity $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.

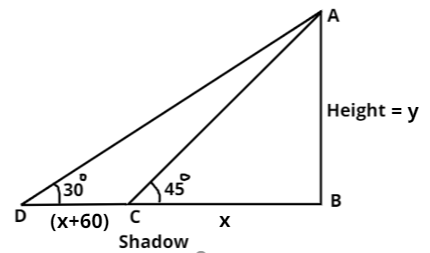
The above figure is drawn with respect to given conditions in question.
Let the height of the tower be AB $= y$ metres.
As we are given that the difference in length of shadows DC (see in figure) is 60 metres.
As, we can see from the above figure that the length of shadow when altitude
of sun is ${45^0}$ $(i.e{\text{ }}\angle {\text{ACB)}}$ be $x$ metres $(i.e{\text{ }}BC)$.
So, length of the shadow when altitude of sun is ${30^0}$ $(i.e{\text{ }}\angle {\text{ADB)}}$ be $\left( {x + 60} \right)$ metres $(i.e{\text{ }}BD)$
As we know that, $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.
So, as we can see from the above figure in $\Delta ABC$ that, $\tan {45^0} = \dfrac{{AB}}{{CB}} = \dfrac{y}{x}$.
So, x = y$$$(i.e{\text{ }}AB = BC)$$ (1) And in $$\Delta ADB$$, \tan {30^0} = \dfrac{{AB}}{{DB}} = \dfrac{{AB}}{{DC + CB}} = \dfrac{y}{{60 + x}}$. Now, putting the value of$\tan {30^0}$and$x$from equation 1 to the above equation. We get,$\dfrac{1}{{\sqrt 3 }} = \dfrac{y}{{60 + y}} \Rightarrow \left( {\sqrt 3 - 1} \right)y = 60 \Rightarrow y = \dfrac{{60}}{{\left( {\sqrt 3 - 1} \right)}} \approx 81.96$metres
Now, as we have defined above that height of the tower is y metres.
Hence, the height of the tower will be 82 metres.

Note: - Whenever we come up with these types of problems then first, we should draw the figure according to the given conditions in question then, we will use the trigonometric functions to get the height of the tower, which will be the easiest and efficient method.