Question
Question: The shadow of a flagstaff is three times as long as the shadow of the flagstaff when the sun rays me...
The shadow of a flagstaff is three times as long as the shadow of the flagstaff when the sun rays meet the ground at an angle of 600. Find the angle between the sun rays and ground at the time of the longer shadow.
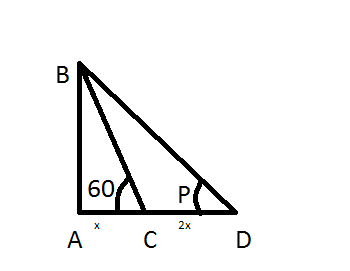
A. P=300
B. P=600
C. P=450
D. P=150
Solution
Hint – In order to solve this problem we need to take two triangles and use the concept of trigonometric angles and get the equations to get the angle P using the trigonometric angles itself.
Complete step-by-step answer:
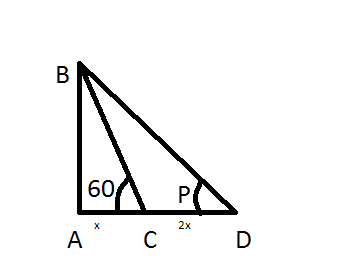
From the given figure AC = x, CD = 2x. Let AB = h and we can clearly see
AD = AC + CD = x + 2x = 3x…………….(1)
In triangle ABC we can say that,
In triangle ABD we can say that,
⇒tanP = ADAB ⇒tanP = 3xh ⇒tanP = 3xx3=31..................(From (2))
So, angle P = 30 degrees.
Hence the right option is A.
Note – To solve this problem we found the relation between h and x and then use the obtained relation in order to calculate angle P here we have used the values that tan60=3 and tan30=31. Doing this will solve your problem.
