Question

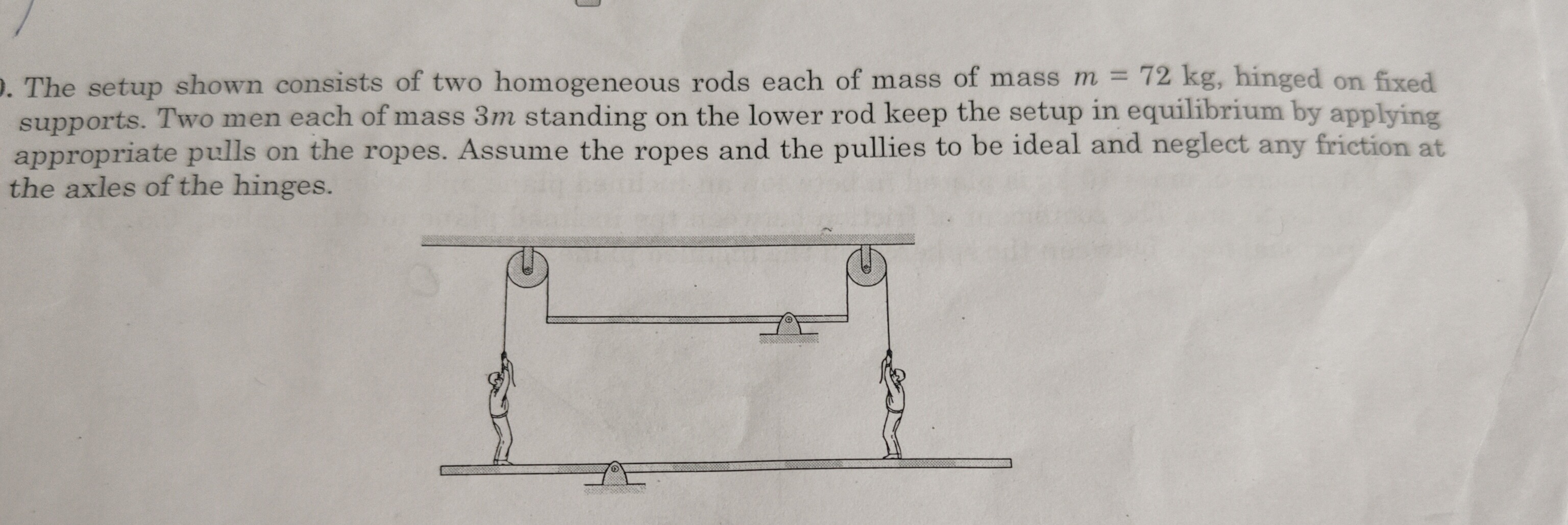
The setup shown consists of two homogeneous rods each of mass of mass $m=72$ kg, hinged on fixed supports. Two men each of mass 3m standing on the lower rod keep the setup in equilibrium by applying appropriate pulls on the ropes.

Answer 1

The question is underspecified due to conflicting information in the diagram and text regarding the upper rod's equilibrium and missing positional information for the men on the lower rod. Based on the direct interpretation of the diagram for the upper rod's rotational equilibrium, the tension in the left rope ($T_L$) must be zero. The tension in the right rope ($T_R$) cannot be determined without knowing the positions of the men on the lower rod.

The problem requires clarification or additional information to provide a specific numerical answer for the "appropriate pulls".

Answer 2

The setup consists of an upper rod hinged at its center, a lower rod hinged at its left end, and two men on the lower rod pulling ropes.

1. Upper Rod Analysis: The upper rod is homogeneous (weight $mg$ at its center) and hinged at its center. The rope from the left man passes over a pulley and is shown attached to the left end of the upper rod. If the rope pulls downwards on the rod (as implied by the man pulling down on the rope, and the rope passing over the pulley), this force $T_L$ would create a clockwise torque about the central hinge. Since the rod's weight and the hinge reaction act at the center, they produce no torque. For the upper rod to be in rotational equilibrium, the net torque must be zero. This implies that the torque due to $T_L$ must be zero, which means $T_L$ must be zero.

2. Contradiction: The problem states that "Two men... keep the setup in equilibrium by applying appropriate pulls on the ropes." The word "pulls" (plural) implies both men are pulling, meaning $T_L \ne 0$. This contradicts the conclusion from the upper rod's FBD.

3. Underspecified Problem: If we assume $T_L=0$ based on the strict interpretation of the diagram, then the left man is simply standing on the lower rod, exerting a normal force $N_L = 3mg$. To determine the tension $T_R$ from the right man, we would need to analyze the lower rod's equilibrium. However, the exact positions of the men on the lower rod are not provided, making the torque balance equation for the lower rod unsolvable for $T_R$ uniquely.

Due to the contradiction in the problem statement/diagram and the lack of specific positional information, a unique numerical answer cannot be determined without making additional assumptions not explicitly given.