Question

The sets E = {All even numbers} and O = {All odd numbers} are
A.Null Sets
B.Singleton Sets
C.Disjoint Sets
D.Overlapping Sets

Answer 1

This question is related with the basics of ‘Set theory’. By understanding the following definitions, we can easily give the answer to it.
Null set: The set which has no element in it is called a null set. Null set is also known as an empty set. It is denoted by $\phi$ .
Singleton set: The set which has one and only one element in it is called a singleton set.
Disjoint sets: Suppose there are two sets A and B. If no element in both sets A and B is common, then the sets A and B are called disjoint sets.
Overlapping sets: Suppose there are two sets A and B. If at least one element in both sets A and B is common, then the sets are called overlapping sets.

Complete step-by-step answer:
It is given that; the set E contains all even numbers in it.
So, E = \left\\{ {2,4,6,8,10, \ldots } \right\\} \ldots \left( i \right)
It is also given that; the set O contains all odd numbers in it.
So, O = \left\\{ {1,3,5,7,9, \ldots } \right\\} \ldots \left( {ii} \right)
Hence, from equations (i) and (ii), It is clear that no element of the sets E and O are similar.
Thus, the sets E and O are disjoint sets.

Note: The sets can also be represented by venn – diagram method. Venn – diagram method is a pictorial representation of the sets in different conditions.
Hence, the given condition using the venn – diagram can be represented as below.

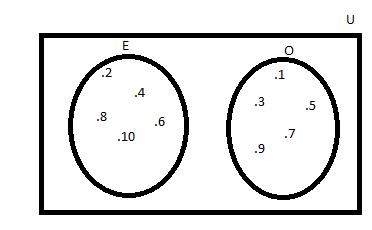
Here, we can see that none of the elements of set E and set O are the same. Hence, both sets will not touch each other and hence they are disjoint sets.