Question

The set of real values of k for which the lines $x+3y+1=0,kx+2y-2=0$ and $2x-y+3=0$ form a triangle is
(a) R-\left\\{ -4,\dfrac{2}{3} \right\\}
(b) R-\left\\{ -4,\dfrac{-6}{5},\dfrac{2}{3} \right\\}
(c) R-\left\\{ -\dfrac{2}{3},4 \right\\}
(d) $R$

Answer 1

Hint:The standard equation of any line is given by $y=mx+c$, here the points of this equation is (x, y). After this we will apply comparison between the given equations with the formula of a line. We will perform such method so that we will solve the solution further.

Complete step-by-step answer:
Now consider the standard equation of line is $y=mx+c....(i)$ and consider the given equation $x+3y+1=0$ which by taking y term one side and x term on the other side is equal to a constant.
$\begin{aligned} & \Rightarrow 3y=-x-1 \\\ & \Rightarrow y=\dfrac{-1}{3}x-1 \\\ \end{aligned}$
Comparing this equation to equation $(i)$ we get the slope of this equation equal to $\dfrac{-1}{3}$.
Similarly, the slope of equation $kx+2y-2=0$ is carried out by taking y term one side and x term on the other side of equal with a constant.
$\begin{aligned} & \Rightarrow 2y=-kx+2 \\\ & \Rightarrow y=\dfrac{-k}{2}x+1 \\\ \end{aligned}$
So the slope is $\dfrac{-k}{2}$ and also, the slope of equation $2x-y+3=0$ is carried out by taking y term one side, x term on the other side of equal with a constant $y=2x+3$ and therefore the slope is 2 here.
Here the slope $\dfrac{-k}{2}\ne 2,\dfrac{-k}{2}\ne \dfrac{-1}{3}$ and this implies that the slope $k\ne -4,k\ne \dfrac{2}{3}$.
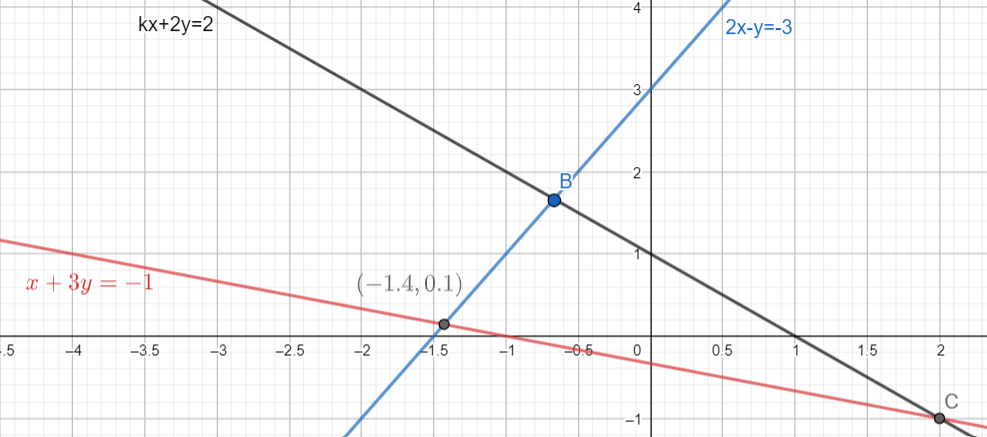
The intersection of the lines $x+3y+1=0$ and $2x-y+3=0$ would satisfy the third line$kx+2y-2=0$ if it is intersecting these lines. But here is a triangle so only two of these lines intersect and the third one will not. So, let us consider that $x+3y+1=0$ and $2x-y+3=0$ intersect and the third equation of line $kx+2y-2=0$ does not intersect.
Now let $x+3y+1=0...(ii)$ and $2x-y+3=0...(iii)$ and multiply $(iii)$ by number 3 and we get a new equation $6x-3y+1=0...(iv)$
Solving $(ii)$ and $(iv)$ we have,
$\begin{aligned} & 6x{-3y}+9=0 \\\ & \,1\underline{x{+3y}+1=0} \\\ & 7x\,\,\,\,\,\,\,\,\,+10=0 \\\ & \Rightarrow 7x=-10 \\\ & \Rightarrow x=\dfrac{-10}{7} \\\ \end{aligned}$
The value of x is approximately equal to -1.4. Now substitute the value in equation $(ii)$ we get,
$\begin{aligned} & x+3y+1=0 \\\ & \Rightarrow \dfrac{-10}{7}+3y+1=0 \\\ & \Rightarrow 3y=\dfrac{10}{7}-1 \\\ & \Rightarrow 3y=\dfrac{10-7}{7} \\\ & \Rightarrow 3y=\dfrac{3}{7} \\\ \end{aligned}$
Therefore $y=\dfrac{1}{7}$ and the value of y is approximately equal to 0.1. So the intersection point between $(ii)$ and $(iii)$ is $\left( \dfrac{-10}{7},\dfrac{1}{7} \right)$ or (-1.4, 0.1).
Now substitute this point in equation $kx+2y-2=0$ with the remembrance that this point is not going to satisfy the equation since it is a triangle. So we get,
$\begin{aligned} & kx+2y-2\ne 0 \\\ & \Rightarrow k\left( \dfrac{-10}{7} \right)+2\left( \dfrac{1}{7} \right)-2\ne 0 \\\ & \Rightarrow \dfrac{-10k}{7}\ne 2-\dfrac{2}{7} \\\ & \Rightarrow \dfrac{-10k}{7}\ne \dfrac{14-2}{7} \\\ & \Rightarrow \dfrac{-10k}{7}\ne \dfrac{12}{7} \\\ & \Rightarrow -10k\ne 12 \\\ & \Rightarrow k\ne \dfrac{-6}{5} \\\ \end{aligned}$
Thus clearly we have three points out of all real numbers to which the value of k is not equal. Therefore we have three values $k\ne -4,k\ne \dfrac{2}{3}$ and $k\ne \dfrac{-6}{5}$ with which k is not equal.
Hence the correct option is (b).

Note: The figure of the required triangle is drawn below.

Alternatively we could have solved it by the formula for slope. But here no points are given directly. That is why the method of comparing equations with the standard equation of line is used here. Taking figure as a guide the formula of the slope is given by $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and after comparing any of the three equations with standard equation of line don’t forget to find the third value of $k\ne \dfrac{-6}{5}$ by substitution in equation $kx+2y-2\ne 0$ because after finding only two points of $k\ne -4,k\ne \dfrac{2}{3}$ can lead to option (a) which is wrong. This is important to note that $kx+2y-2\ne 0$ should not be confused with $kx+2y-2=0$ and the equation $kx+2y-2\ne 0$ is used here to find that value of which does not satisfy this equation.