Question

The set of points on the axis of the parabola 2\left\\{ {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}} \right\\}={{\left( x+y \right)}^{2}} from which three distinct normals can be drawn is the set of points $\left( h,k \right)$ lying on the axis of the parabola, such that$$$$
A.h>\dfrac{3}{2}$$$$$ B. h>2 C. $h>4
D. $k<\dfrac{3}{2}$$$$$

Answer 1

We know that if the coordinate of the vertex is given by $V\left( m,n \right)$ then we can only draw the there normals on a point $\left( x,y \right)$ the axis when $x>3m,y>1.5n$. We compare the equation of parabola with standard equation of parabola in focus-directrix form to get the vertex and then find condition on $h.$$$$$

Complete step-by-step solution
We know that parabola is the locus of a point which moves such that its distance from a fixed point is equal to its distance from a fixed line. The fixed line is called directrix and the fixed point is called focus. We know that if the focus of the parabola is $F\left( a,b \right)$ and the equation of directrix is $lx+my+n=0$ then we can write the equation of the parabola in focus-directrix form as
${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{\dfrac{\left( lx+my+c \right)}{{{l}^{2}}+{{m}^{2}}}}^{2}}$

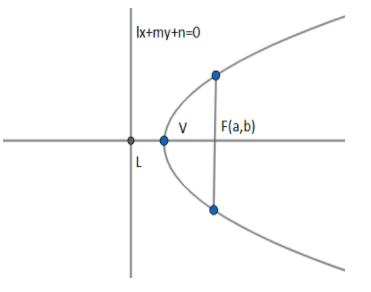
The line perpendicular to directrix is called axis and the midpoint of $L\left( c,d \right)$ and the focus F is called vertex $V\left( \dfrac{a+c}{2},\dfrac{b+d}{2} \right)$. The line perpendicular to the axis passing through the focus is called latus rectum . We know that we can only draw three only normals to the parabola form the axis on a point $\left( {{x}_{1}},{{y}_{2}} \right)$ beyond twice the latus rectum from vertex which in this case is,
${{x}_{1}}>3\left( \dfrac{a+c}{2} \right),{{y}_{1}}>\dfrac{3}{2}\left( \dfrac{b+d}{2} \right)$

The given equation of the parabola is
2\left\\{ {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}} \right\\}={{\left( x+y \right)}^{2}}
Let us convert the above equation to the standard form and to the focus-directrix form and have,
\left\\{ {{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}} \right\\}=\dfrac{{{\left( x+y \right)}^{2}}}{2}
We compare the above equation with standard equation with focus and directrix and have coordinates of focus as $\left( a,b \right)=\left( 1,1 \right)$ where the equation of the directrix is $x+y=0\Rightarrow x=-y$ . The directrix passes through the origin at an angle ${{\tan }^{-1}}\left( \dfrac{-1}{1} \right)={{135}^{\circ }}$ with a positive $x-$axis. The coordinate of L is $L\left( 0,0 \right)=L\left( c,d \right)$. So the vertex is
$V\left( \dfrac{c+a}{2},\dfrac{d+b}{2} \right)=V\left( \dfrac{0+1}{2},\dfrac{0+1}{2} \right)=V\left( \dfrac{1}{2},\dfrac{1}{2} \right)$
We have any point on the axis as $\left( h,k \right)$, hence the condition is
$h>3\left( \dfrac{a+c}{2} \right)=3\left( \dfrac{1+0}{2} \right)=\dfrac{3}{2}$

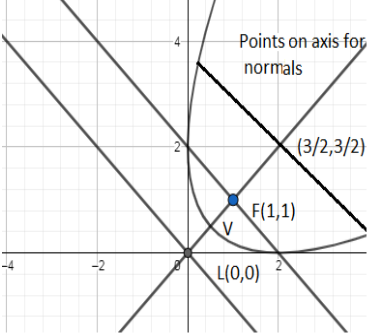
So the correct option is A.

Note: The condition for $k$ is $k>\dfrac{3}{4}$. We can alternatively solve by shifting the standard parabola ${{y}^{2}}=4ax$ by ${{45}^{\circ }}$ in an anti-clockwise direction. The equation of normals to the parabola ${{y}^{2}}=4ax$ with slope $m$ is given by $y=mx-2m-{{m}^{3}}$.