Question

The set of equations $y = \lambda x + \cos \theta z, 4x + 2y + z = x + y - z$ $(\cos \theta)x + y + 2z = 0, 0 \leq \theta < 2\pi$, has non-trivial solution(s)

Answer 1

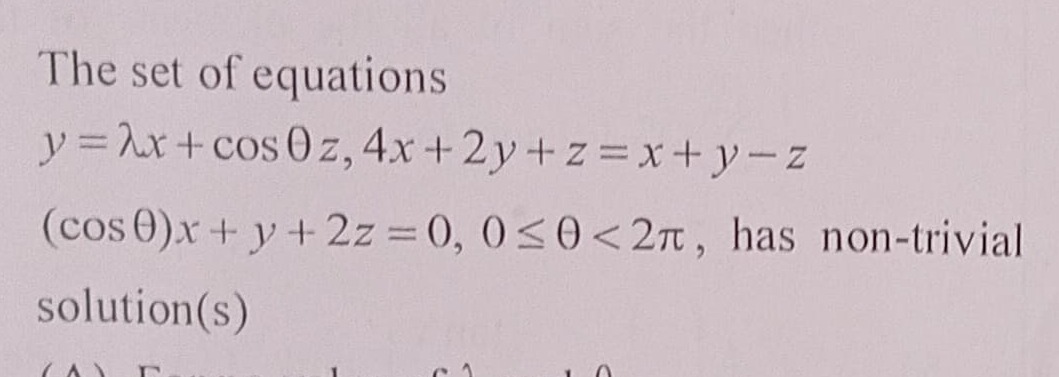
No non-trivial solutions

Answer 2

To determine if the given system of linear equations has non-trivial solutions, we first need to write the equations in the standard homogeneous form $Ax + By + Cz = 0$.

The given equations are:

1. $y = \lambda x + \cos \theta z$
2. $4x + 2y + z = x + y - z$
3. $(\cos \theta)x + y + 2z = 0$

Rewrite them in the standard form:

1. $\lambda x - y + (\cos \theta) z = 0$
2. $4x - x + 2y - y + z - (-z) = 0 \Rightarrow 3x + y + 2z = 0$
3. $(\cos \theta)x + y + 2z = 0$

Now, form the coefficient matrix $A$ for this homogeneous system: $A = \begin{pmatrix} \lambda & -1 & \cos \theta \\ 3 & 1 & 2 \\ \cos \theta & 1 & 2 \end{pmatrix}$

For a homogeneous system of linear equations to have non-trivial solutions, the determinant of the coefficient matrix must be zero, i.e., $\det(A) = 0$.

Calculate the determinant of $A$: $\det(A) = \lambda \begin{vmatrix} 1 & 2 \\ 1 & 2 \end{vmatrix} - (-1) \begin{vmatrix} 3 & 2 \\ \cos \theta & 2 \end{vmatrix} + (\cos \theta) \begin{vmatrix} 3 & 1 \\ \cos \theta & 1 \end{vmatrix}$

$\det(A) = \lambda (1 \cdot 2 - 2 \cdot 1) + 1 (3 \cdot 2 - 2 \cdot \cos \theta) + (\cos \theta) (3 \cdot 1 - 1 \cdot \cos \theta)$

$\det(A) = \lambda (2 - 2) + (6 - 2 \cos \theta) + (3 \cos \theta - \cos^2 \theta)$

$\det(A) = \lambda (0) + 6 - 2 \cos \theta + 3 \cos \theta - \cos^2 \theta$

$\det(A) = 6 + \cos \theta - \cos^2 \theta$

Now, set the determinant to zero to find the conditions for non-trivial solutions: $6 + \cos \theta - \cos^2 \theta = 0$

Multiply by -1 to rearrange the terms into a standard quadratic form: $\cos^2 \theta - \cos \theta - 6 = 0$

Let $u = \cos \theta$. The equation becomes a quadratic equation in $u$: $u^2 - u - 6 = 0$

Factorize the quadratic equation: $(u - 3)(u + 2) = 0$

This gives two possible values for $u$: $u = 3$ or $u = -2$

Substitute back $u = \cos \theta$: $\cos \theta = 3$ or $\cos \theta = -2$

However, the range of the cosine function for real values of $\theta$ is $[-1, 1]$. That is, $-1 \leq \cos \theta \leq 1$. Neither $\cos \theta = 3$ nor $\cos \theta = -2$ falls within this valid range.

Since there are no real values of $\theta$ for which $\cos \theta = 3$ or $\cos \theta = -2$, the determinant $\det(A)$ is never equal to zero for any real $\theta$.

Therefore, the system of equations never has non-trivial solutions. It only possesses the trivial solution ($x=0, y=0, z=0$).