Question

The set of all points where the function $f\left( x \right) = \sqrt {{x^2}|x|}$is differentiable is
A.$[0,\infty )$
B.$\left( {0,\infty } \right)$
C.$\left( { - \infty ,\infty } \right)$
D.$\left( { - \infty ,0} \right) \cup \left( {0,\infty } \right)$

Answer 1

For the given function find the domain of the function, for the values of domain plot a graph, provided that to find the set of all points where the function $f\left( x \right) = \sqrt {{x^2}|x|}$is differentiable, and finds the set of points with the help of the graph.

Complete step-by-step answer:
For the given function $f\left( x \right) = \sqrt {{x^2}|x|}$, let's find the domain of the function.
For $|x| = x$,where$x \geqslant 0$ the function will be
$\Rightarrow f\left( x \right) = \sqrt {{x^2}|x|} \\\ \Rightarrow f\left( x \right) = \sqrt {{x^3}} \\\ \Rightarrow f\left( x \right) = x.......\left( 1 \right) \\\$
So, the values of the function lie between $\left( {0,\infty } \right)$.
For $|x| = - x$,where$x < 0$ the function will be
$f\left( x \right) = \sqrt {{x^2}|x|} \\\ \Rightarrow f\left( x \right) = \sqrt {{x^2}\left( { - x} \right)} \\\ \Rightarrow f\left( x \right) = \sqrt { - {x^3}} \\\ \Rightarrow f\left( x \right) = - x........\left( 2 \right) \\\$
So, the values of the function lie between $\left( { - \infty ,0} \right)$.
So, the domain of the function is $\left( { - \infty ,0} \right) \cup \left( {0,\infty } \right)$.
Plot a graph with the help of (1) and (2), i.e. $y = - x\,and\,y = x$

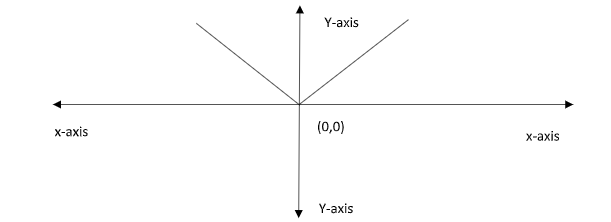
So, from the graph it is clearly indicating that the set of all points where the function $f\left( x \right) = \sqrt {{x^2}|x|}$ is differentiable $\left( { - \infty ,0} \right) \cup \left( {0,\infty } \right)$.
So, option D is correct.

Note: Point to remember: When a function lies between x and y, then x and y are not included in the domain values.