Question

The set $\left( {A \cup B \cup C} \right) \cap \left( {A \cap {B^\prime } \cap {C^\prime }} \right) \cap {C^\prime }$ is equal to?
A) $B \cap {C^\prime }$
B) $A \cap C$
C) ${B^\prime } \cap {C^\prime }$
D) None of these

Answer 1

In this problem we use union, intersection & complement concepts .We can solve this by Venn diagram.
Definition of union: The union of two sets A & B is a set containing all elements that are from A & B. It is denoted by
$A \cup B$
Definition of intersection: The intersection of two sets A & B; consist of all the elements that are both in A & B. Means the intersection is the common region between A & B. The intersection is denoted by $A \cap B$.
Definition of complement: The complement of a set A is the set of all elements that are in the universal set U but are not in A. it is denoted by ${A^c}$.

Complete step-by-step answer:

1. First we will draw the Venn diagram of $\left( {A \cup B \cup C} \right)$
   
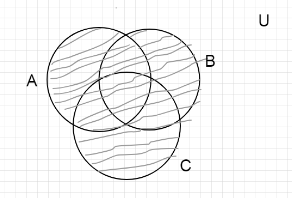
   So, we can see that this set contains all the forms A, B, C.
2. Next, we will draw a diagram of $\left( {A \cap {B^\prime } \cap {C^\prime }} \right)$
   
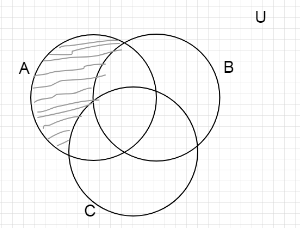
   By the definition of the complement, we can see in this set there are no any elements which are contained in B & C.
3. Here we will draw a diagram of ${C^\prime }$.
   
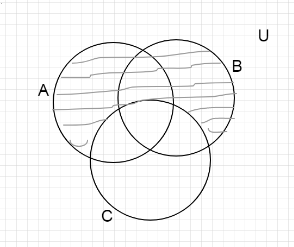
   This set contains all the elements in A & B except the elements which are in C.
   Now, we have to find $\left( {A \cup B \cup C} \right) \cap \left( {A \cap {B^\prime } \cap {C^\prime }} \right) \cap {C^\prime }$
   For that we will take the intersection of the above three diagrams. Means, we will consider the common region from these three diagrams.
   
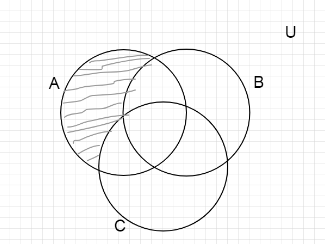
   We get this above region. But it is same as $\left( {A \cap {B^\prime } \cap {C^\prime }} \right)$
   Here, option C is same as $\left( {A \cap {B^\prime } \cap {C^\prime }} \right)$
   Let us understand this by the venn diagram.
   $\left( {A \cap {B^\prime } \cap {C^\prime }} \right)$ ${B^\prime } \cap {C^\prime }$
   

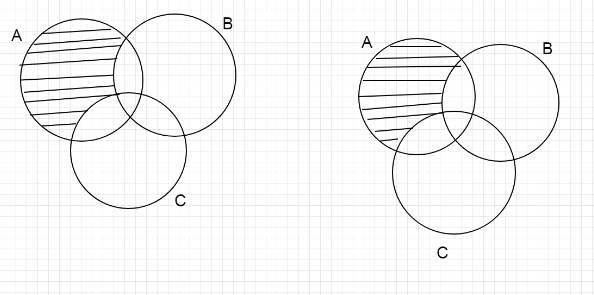
Hence, option C) is the correct answer.

Note: In this type of problems when multiple sets & terms are there, then we have to draw a diagram step by step. Then we will get the proper answer. Students should be perfect at the concept of union, intersection & complement.