Question
Question: The roots $\alpha$, $\beta$ of the quadratic equation $ax^2 + bx + c = 0, a \neq 0$ lie in the inter...
The roots α, β of the quadratic equation ax2+bx+c=0,a=0 lie in the interval [0, 1], then?
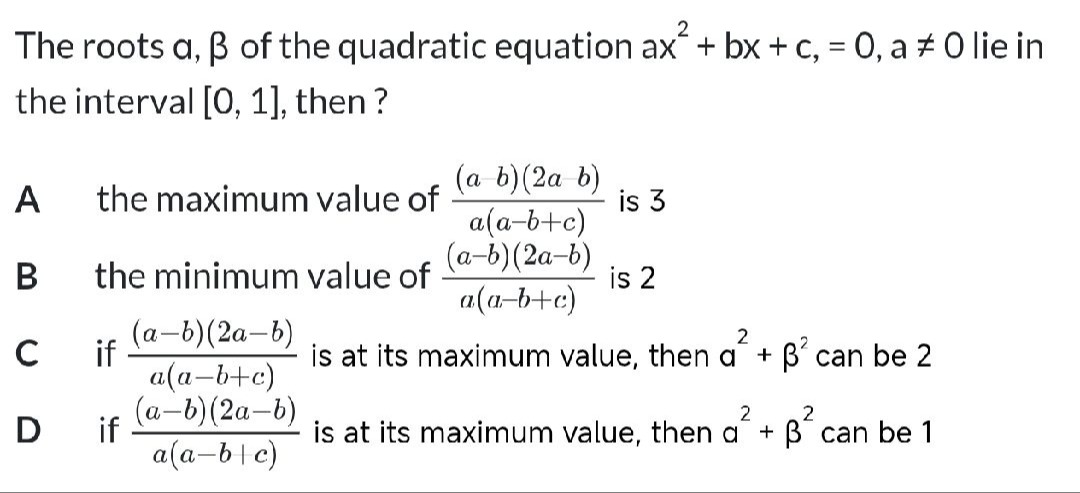
the maximum value of a(a−b+c)(a−b)(2a−b) is 3
the minimum value of a(a−b+c)(a−b)(2a−b) is 2
if a(a−b+c)(a−b)(2a−b) is at its maximum value, then α2+β2 can be 2
if a(a−b+c)(a−b)(2a−b) is at its maximum value, then α2+β2 can be 1
A, B, C, D
Solution
The expression E=a(a−b+c)(a−b)(2a−b) can be rewritten in terms of the sum of roots S=α+β and the product of roots P=αβ as E=1+S+P(1+S)(2+S). The condition that the roots α,β lie in the interval [0, 1] implies the following constraints on S and P:
- 0≤S≤2
- 0≤P≤1
- P≤S2/4 (from the discriminant condition for real roots)
- P≥S−1 (from the condition that roots lie in [0,1])
Combining these, the feasible region for (S,P) is max(0,S−1)≤P≤min(1,S2/4).
To find the maximum value of E, we need to minimize the denominator 1+S+P. This occurs when P is at its minimum, Pmin=max(0,S−1).
- For 0≤S<1, Pmin=0, so E=1+S+0(1+S)(2+S)=2+S. The maximum value in this range approaches 2+1=3 as S→1.
- For 1≤S≤2, Pmin=S−1, so E=1+S+(S−1)(1+S)(2+S)=2S(1+S)(2+S). At S=1, E=2(2)(3)=3. At S=2, E=4(3)(4)=3. The function 2S(1+S)(2+S) has a minimum at S=2 and maximums at S=1 and S=2.
The overall maximum value of E is 3. This occurs when (S,P)=(1,0) (roots are 0 and 1) or (S,P)=(2,1) (roots are 1 and 1). So, option A is correct.
To find the minimum value of E, we need to maximize the denominator 1+S+P. This occurs when P is at its maximum, Pmax=S2/4 (since S2/4≤1 for S∈[0,2]). E=1+S+S2/4(1+S)(2+S)=(1+S/2)2(1+S)(2+S)=(2+S)24(1+S)(2+S)=2+S4(1+S). Let g(S)=2+S4(1+S). This function is increasing for S∈[0,2] (g′(S)=(2+S)24>0). The minimum value occurs at S=0, where g(0)=24(1)=2. This occurs when (S,P)=(0,0) (roots are 0 and 0). The overall minimum value of E is 2. So, option B is correct.
Now consider options C and D, which are conditional statements about α2+β2 when E is at its maximum value of 3. The maximum value of E=3 occurs in two cases:
- S=1,P=0: The roots are α=0,β=1. In this case, α2+β2=02+12=1.
- S=2,P=1: The roots are α=1,β=1. In this case, α2+β2=12+12=2.
Therefore, if E is at its maximum value, α2+β2 can be 1 (Option D is correct) and α2+β2 can be 2 (Option C is correct).
All four options are correct.
