Question

The rod of weight $W$ is supported by two parallel knife edges $A$ and $B$ is in equilibrium in horizontal position. The knives are at a $d$ distance d from each other. The center of the mass of a rod is at distance $x$ from the $A$. The normal reaction on $A$ is,
(A) $\dfrac{W(d-x)}{x}$
(B) $\dfrac{W(d-x)}{d}$
(C) $\dfrac{Wx}{d}$
(D) $\dfrac{Wd}{x}$

Answer 1

The rod is supported by two identical knives edges. Here the position of the center of mass is also given. The system is in equilibrium therefore all the forces are balanced and torque at all points is zero. So the question will be solved by a combination of Newton’s third law of motion and torque acting on the given system.

Formula used:
${{F}_{x}}(\uparrow )={{F}_{x}}(\downarrow )$
And $\tau =r\times f$

Complete answer:
The rod of weight $W$ is supported by two parallel knife edges $A$ and $B$ is in equilibrium in horizontal position, the knives are at a $d$ distance d from each other, the center of the mass of a rod is at distance $x$ from the $A$, are as shown in figure.
The forces of the system is in equilibrium in $x$ direction,

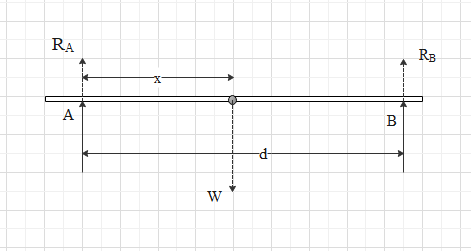
From the Newton’s third law of motion
${{R}_{A}}+{{R}_{B}}=W$ $.....(1)$
And for that torque about $B$knife is zero,
$(d-x)W+d{{R}_{A}}=0$ $.....(2)$
$\therefore {{R}_{A}}=\dfrac{(d-x)W}{d}$

So, the correct answer is “Option B”.

Note:
Torque is the measure of the force which can rotate the body about any particular axis and torque is the cause of angular acceleration. Hence here the system is in equilibrium therefore no angular acceleration in any part of the system. So the torque by knife $A$ is zero.