Question

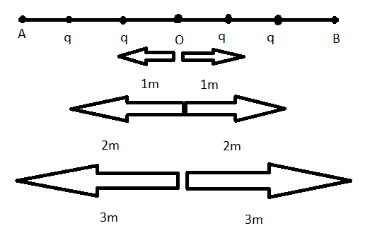
The rod is rotated uniformly about an axis passing through O and perpendicular to its length such that the linear speed of the end A or B of the rod is $3m{s^{ - 1}}$ . Magnetic field at O is:
A.\dfrac{{11{\mu _0}q}}{{12\pi }} \\\ B.\dfrac{{3{\mu _0}q}}{{7\pi }} \\\ C.\dfrac{{{\mu _0}q}}{{2\pi }} \\\ D.\dfrac{{6{\mu _0}q}}{{13\pi }} \\\

Answer 1

Hint : We use the formula to calculate the magnetic field of the rod at the center. Since it's rotating it behaves like a circular ring. Putting the value for current in the magnetic field and then calculate for each dotted charge, hence calculating the net magnetic field.

Complete Step By Step Answer:
In order to solve this question we see that linear speed is given on one end of the rod that is A or B equal to $3m{s^{ - 1}}$ .
Here q is the charge on the rod AB.
Now we know that rotation takes place only at the dotted q points.
During the rotation we can see the rod as a circular ring and we also know that the magnetic field if the circular wire ring at the center of a current carrying is equal to $B = \dfrac{{{\mu _0}I}}{{2r}}$ .
Also current here;
I = \dfrac{q}{T} \\\ = \dfrac{{qv}}{{2\pi r}} \\\
Where T is the time period.
So putting the value of current in the above, we get;
$B = \dfrac{{{\mu _0}qv}}{{4\pi {r^2}}}$
The charge q present at $1m$ distance from zero, will have circular path of the magnetic field with radius $1m$ , and likewise for $2m$ and $3m$ radius.
Also velocity at one meter distance is equal to $1m{s^{ - 1}}$ .
Now calculating the net magnetic field, we get;
{B_{net}} = \dfrac{{{\mu _0}q}}{{4\pi }}(2 \times \dfrac{1}{{{1^2}}} + 2 \times \dfrac{2}{{{2^2}}} + 2 \times \dfrac{3}{{{3^2}}}) \\\ {B_{net}} = \dfrac{{{\mu _0}q}}{{2\pi }}(\dfrac{1}{{{1^2}}} + \dfrac{1}{2} + \dfrac{1}{3}) \\\ = \dfrac{{{\mu _0}q}}{{2\pi }}(\dfrac{{11}}{6}) \\\ = \dfrac{{11{\mu _0}q}}{{12\pi }} \\\
Hence option A is the correct answer.

Note :
We know that rotation takes place only at the dotted q points.
During the rotation we can see the rod as a circular ring and we also know that the magnetic field if the circular wire ring at the center of a current carrying is equal to $B = \dfrac{{{\mu _0}I}}{{2r}}$ .