Question

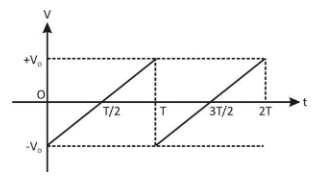
The rms value for the saw-tooth voltage of peak value ${V_0}$ from $t = 0$ to $t = 2T$ as shown in the figure is $\dfrac{{{v_0}}}{{\sqrt x }}$. Find the value of x.

Answer 1

In this question, we need to determine the value of ‘x’ such that $\dfrac{{{v_0}}}{{\sqrt x }}$ is the rms value of the saw-tooth voltage of peak value ${V_0}$ from $t = 0$ to $t = 2T$. For this, we will use the definition of the rms value of the wave and compare the rms value given in the question with the calculated value.

Complete step by step answer:
The rms value is defined as the square root of the mean value of the squared function. If ${T_P}$ is the time period of the wavefront then, the rms value is given as
${V_{RMS}} = \dfrac{1}{{{T_P}}}\int_0^{{T_P}} {{v^2}dt} {\text{ - - - - }}(i)$
On working the equation (i) for calculating the rms value, we will get the equation of ‘v’ in the function of time ‘t’.

Let’s have a look straight line $BC$in the graph, the slope of this line is $m = \dfrac{{{V_0}}}{{\left( {\dfrac{T}{2}} \right)}} = \dfrac{{2{V_0}}}{T}$, so the equation of this straight line is given by the equation,
$g = mx + C \\\ \Rightarrow V = \dfrac{{2{v_0}}}{T}t + ( - {v_0}) \\\ \Rightarrow V = \dfrac{{2{v_0}t}}{T} = {v_0} \\\$
Now, substituting the value of ‘v’ in the equation (i) we get

$$\Rightarrow\int_0^{{T_P}} {{v^2}dt} = {\int_0^T {\left( {\dfrac{{2{v_0}t}}{T} - {v_0}} \right)} ^2}dt\,\,\,\,\,\,\,\,(\because {T_P} = T) \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \int_0^T {\left[ {{{\left( {\dfrac{{2{v_0}t}}{T}} \right)}^2} + v_0^2 - 2 \times \dfrac{{2{v_0}t}}{T} \times {V_0}} \right]} dt \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \int_0^T {\left( {\dfrac{{4v_0^2{t^2}}}{{{T^2}}} + v_0^2 - \dfrac{{4v_0^2t}}{T}} \right)} dt \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \dfrac{{4v_0^2}}{T}\int_0^T {{t^2}dt + v_0^2\int_0^2 {dt - \int_0^T t } \,dt} \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \dfrac{{4v_0^2}}{{{T^2}}}{\left[ {\dfrac{{{t^3}}}{3}} \right]^T} + v_0^2[t]_0^T - \dfrac{{4v_0^2}}{T}\left[ {\dfrac{{{t^2}}}{2}} \right]_0^T \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \dfrac{{4v_0^2}}{{{T^2}}}\left[ {\dfrac{{{T^3}}}{3}} \right] + v_0^2[T] -\dfrac{{4v_0^2}}{T}\left[ {\dfrac{{{T^2}}}{2}} \right] \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \dfrac{{4v_0^2T + 6v_0^2T - 12v_0^2T}}{6} \\\ \Rightarrow\int_0^{{T_P}} {{v^2}dt}= \dfrac{{14v_0^2T - 12v_0^2T}}{6} - - - - - (ii) \\\$$

Divided both sides by T of equation (i)
$\dfrac{1}{T}\int_0^{{T_P}} {{v^2}dt} = \dfrac{{v_0^2}}{3} - - - - (iii)$
Taking under the root of both the sides in equation (ii)
$\sqrt {\dfrac{1}{T}\int_0^{{T_P}} {{v^2}dt} } = \sqrt {\dfrac{{v_0^2}}{3}}$
As, $T = {T_P}$ so, the above equation can be written as:
$\therefore\sqrt {\dfrac{1}{{{T_P}}}\int_0^{{T_P}} {{v^2}dt} } = \dfrac{{{v_0}}}{{\sqrt 3 }} - - - - (iv)$
Comparing the equation (1) and (4), we can say that ${V_{rms}} = \dfrac{{{v_0}}}{{\sqrt 3 }}$.
According to the question, ${V_{rms}} = \dfrac{{{v_0}}}{{\sqrt x }} = \dfrac{{{v_0}}}{{\sqrt 3 }}$
Hence, $x = 3$.

Note: The rms value is the effective value of a varying voltage or current. It is equivalent to steady DC (constant) value which gives the same effect. The rms stands for root mean square, and it is a way of expressing AC quantity of voltage or current in terms functionally equivalent to DC.