Question

The right circular cylinder of radius $r$ $cm$ and height $h$ $cm$ ( where $h > 2r$) just encloses the sphere of diameter ( in $cm$):
A. $r$
B. $2r$
C. $h$
D. $2h$

Answer 1

Draw the diagram and you will come to a relation between the diameter of the right circular cylinder and the sphere enclosed and then you will get your answer.

Complete step-by-step answer:
In this question it is said that there is the right circular cylinder of radius $r$ $cm$ and height $h$ $cm$ which just encloses the sphere and we need to find its diameter.
And it is also given that $h > 2r$.
So if any object needs to enclose others then their volume must be greater than the enclosed object volume.
So let us check
Volume of right circular cone $\geqslant$ volume of the sphere enclosed.
Let radius of the sphere be $R$
$\pi {r^2}h \geqslant \dfrac{4}{3}\pi {R^3}$
And it is also given that $h > 2r$.
Let us take $h = 2r$
Then $\pi {r^2}\left( {2r} \right) \geqslant \dfrac{4}{3}\pi {R^3}$
$2{r^3} \geqslant \dfrac{4}{3}{R^3}$
${R^3} \leqslant \dfrac{3}{2}{r^3}$
$R \leqslant {\left( {\dfrac{3}{2}} \right)^{\dfrac{1}{3}}}r$
Now let us draw the diagram of the right circular cylinder and the enclosed sphere.

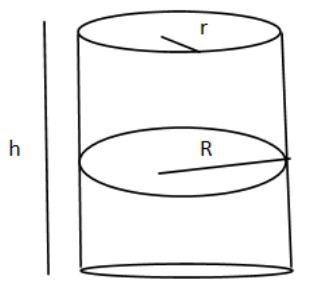
As $h > 2r$, hence we can say that $R = r$ so that it encloses the sphere.
Now diameter is asked in the question which is twice the radius which is $2r$.
Diameter = $2r$

So, the correct answer is “Option B”.

Note: If we enclose the sphere into the right circular cylinder and it is given that $h > 2r$, then by observation also we can say that both have the same radius. Hence diameter will be $2r$.