Question

The resultant R of two forces acting on a particle is at right angles to one of them and its magnitude is one third of the other force. The ratio of larger force to smaller one is:
(A) 2:1
(B) 3:2$\sqrt{2}$
(C) 3:2
(D) 3:$\sqrt{2}$

Answer 1

The resultant of the two forces is given with the help of parallelogram law of vector addition. A parallelogram can be formed, and as one of the angles is already a right angle, Pythagora's theorem can be used to find the side of the right triangle formed.

Complete answer:
Let the resultant vector have a magnitude of F/3 and one of the forces have the magnitude of F. Now, considering the following figure.

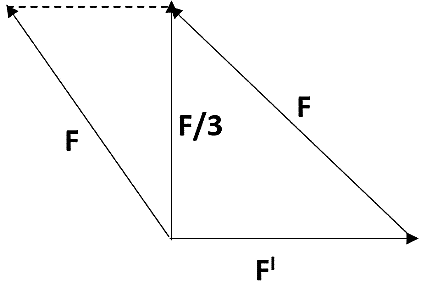
In the figure, the resultant lies in the middle and other vectors are F and F’. F’ is the one we need to find. We can place the force vector F such that it starts at the head of the vector F’ and ends at the head of the resultant vector. In vectors, direction and magnitude is important so we are preserving that in doing so.
Here, the parallelogram gives the magnitude of the remaining force.
The remaining force is given as:
$\sqrt{F^2 - \dfrac{F^2}{9} }= \dfrac{2 \sqrt{2} F}{3}$
Therefore now one of the forces in the question has a magnitude of F and the other force has a magnitude of $3:2 \sqrt{2}$ .

Therefore, the correct answer is option (B).

Note:
There are a lot of similarities between triangle law and parallelogram law of vector addition. In the triangle law, the two forces under consideration are placed in head to tail format while in parallelogram law of vector addition, the two forces are acting at the same point i.e, the tail of both vectors are at the same point. Generally, in questions that deal with forces, parallelogram law is used as a starting point because both the forces act at the same point.