Question

The resultant of two vectors $\overrightarrow P$ and $\overrightarrow Q$ is $\overrightarrow R$ .If the magnitude of $\overrightarrow Q$is doubled, the new resultant vector becomes perpendicular to$\overrightarrow P$ , then the magnitude of $\overrightarrow R$ is equal to
A. P+Q
B. P
C. P-Q
D. Q

Answer 1

A Vector quantity is the physical quantities which have both direction and magnitude. Thus, position vector is referred to as a straight line with one end fixed to the body and other end connected to a moving point and may be used to state the position of a point relative to the body. The displacement vector of a particle is the vector which joins its initial position to the final position. Other examples of vector quantities are force, displacement, velocity, etc.

Complete step by step answer:
$\overrightarrow P$, $\overrightarrow Q$are two vectors. According to question
$\overrightarrow R$is the resultant vector of $\overrightarrow P$ and $\overrightarrow Q$ as shown in the diagram (self made). It means the value of resultant vector ($\overrightarrow R$) is:
$\overrightarrow R$=$\overrightarrow P$+$\overrightarrow Q$

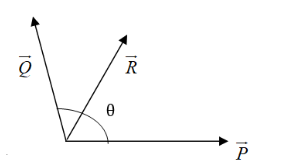
Since we are given that resultant of P and Q is R therefore magnitude of R is given by ${R^2} = {P^2} + {Q^2} + 2PQ\cos \theta$
Where, θ is the angle between $\overrightarrow P$ and $\overrightarrow Q$
If vector$\overrightarrow Q$ is doubled (i.e. 2$\overrightarrow Q$) then new resultant become $\overrightarrow {{R^1}}$ (shown in diagram (self-made)) i.e.:
$\overrightarrow {{R^1}} = \overrightarrow P + 2\overrightarrow Q$

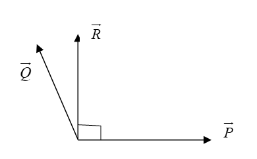
As we know that if one vector is perpendicular to another vector then its dot product is zero so that we can say that:
$\overrightarrow {{R^1}} *\overrightarrow {{P^{^1}}} = 0 \\\ \Rightarrow \left( {\overrightarrow P + 2\overrightarrow Q } \right)*\overrightarrow P = 0 \\\ \Rightarrow {P^2} + 2\overrightarrow Q \overrightarrow P = 0 \\\$
As a result:
$2\overrightarrow Q \overrightarrow P = - {P^2}$ [It should be noted that P is magnitude not the vector] (I)
We know that:
$R = \sqrt {{P^2} + {Q^2} + 2\overrightarrow P \overrightarrow Q }$ [Addition vector rule]
Now substituting the value from equation (i) we get:

$${R^2} = {P^2} + {Q^2} - {P^2} \\\ \therefore {R^2} = {Q^2}$$

This indicates that the magnitude of $\overrightarrow R$ is equal to the magnitude of $\overrightarrow Q$.

Hence, option D is correct.

Note: R and Q both are the magnitude of the vector in the present case so it must have positive value, can’t hold negative value (because angle between two vectors is acute). If the angle between the two vectors is obtuse, their dot product is negative. .Always remember that if one vector is perpendicular with another vector then its dot product is zero i.e. $\overrightarrow R *\overrightarrow P = 0$in the present case. On the other hand if one vector is parallel with another vector, then its dot product is always one.