Question

The resultant of two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is at right angles to $\overrightarrow{A}$ and vector $\overrightarrow{A}$ magnitude is half of that of vector $\overrightarrow{B}$. Find the angle between $\overrightarrow{A}$ and $\overrightarrow{B}$ in degrees.

Answer 1

Hint: This problem can be solved by using the direct formula for the angle made by the resultant of two vectors with one of the vectors. By plugging in the magnitudes of the vectors given and the relation between them, we can get the required answer.

Formula used:
$\phi ={{\tan }^{-1}}\left( \dfrac{Q\sin \theta }{P+Q\cos \theta } \right)$

Complete step by step answer:
We will use the direct formula for the angle made by the resultant of two vectors with one of the vectors and plug in the information given in the question.
The angle $\phi$ made by the resultant of two vectors $\overrightarrow{P}$ and $\overrightarrow{Q}$ with magnitudes $P$ and $Q$ respectively, with $\overrightarrow{P}$ is given by
$\phi ={{\tan }^{-1}}\left( \dfrac{Q\sin \theta }{P+Q\cos \theta } \right)$ --(1)
Where $\theta$ is the angle between $\overrightarrow{P}$ and $\overrightarrow{Q}$.
Now, let us analyze the question.

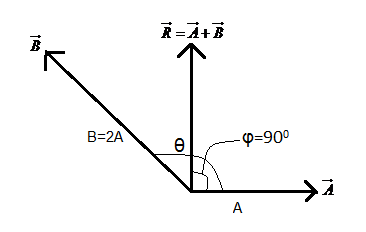
We are given two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$.
Let their resultant be $\overrightarrow{R}$.
Now it is given that $\overrightarrow{R}$ is at right angles to $\overrightarrow{A}$. Hence, the angle between $\overrightarrow{R}$ and $\overrightarrow{A}$ is $\phi ={{90}^{0}}$.
Let the magnitudes of $\overrightarrow{A}$ and $\overrightarrow{B}$ be $A$ and $B$ respectively and the angle between them be $\theta$.
We have to find out $\theta$.
Also according to the question, the vector $\overrightarrow{A}$ magnitude is half of that of the vector $\overrightarrow{B}$.
$\therefore A=\dfrac{1}{2}B$
$\therefore 2A=B$ --(2)
Now, using (1), we get,
$\phi ={{\tan }^{-1}}\left( \dfrac{B\sin \theta }{A+B\cos \theta } \right)$
$\therefore {{90}^{0}}={{\tan }^{-1}}\left( \dfrac{B\sin \theta }{A+B\cos \theta } \right)$
Putting (2) in the above equation, we get,
$\therefore {{90}^{0}}={{\tan }^{-1}}\left( \dfrac{2A\sin \theta }{A+2A\cos \theta } \right)={{\tan }^{-1}}\left( \dfrac{\left( A \right)2\sin \theta }{A\left( 1+2\cos \theta \right)} \right)={{\tan }^{-1}}\left( \dfrac{2\sin \theta }{\left( 1+2\cos \theta \right)} \right)$
$\therefore \tan {{90}^{0}}=\dfrac{2\sin \theta }{1+2\cos \theta }$
$\therefore \dfrac{1}{\tan {{90}^{0}}}=\cot {{90}^{0}}=\dfrac{1+2\cos \theta }{2\sin \theta }$ $\left( \dfrac{1}{\tan \left( \text{angle} \right)}=\cot \left( \text{angle} \right) \right)$
$\therefore 0=\dfrac{1+2\cos \theta }{2\sin \theta }$ $\left( \because \cot {{90}^{0}}=0 \right)$
$\therefore 1+2\cos \theta =0$
$\therefore 2\cos \theta =-1$
$\therefore \cos \theta =-\dfrac{1}{2}$
$\therefore \theta ={{\cos }^{-1}}\left( -\dfrac{1}{2} \right)={{120}^{0}}\text{ or 24}{{\text{0}}^{0}}$
Hence, the angle between $\overrightarrow{A}$ and $\overrightarrow{B}$ can be ${{120}^{0}}\text{ or }{{240}^{0}}$.

Note: Students must be thinking why there are two possible values to the angle between the vectors. This is because it is given that the resultant makes an angle of ${{90}^{0}}$ with $\overrightarrow{A}$. However, it is not mentioned whether it makes the angle in the anticlockwise sense or the clockwise sense. These two possibilities give rise to two possible answers.
This problem could also have been solved by considering an orthogonal coordinate system and comparing the sum of the components of the individual vectors along each axis with that of the component of the resultant along the axis. However, that would have turned out to be a bit of a lengthier process since unnecessary variables in the form of the components of the vectors would have come into the equation and complicated our calculation a bit.