Question

The resultant of two forces is $10\sqrt{7}N$, when one of the forces will be $10\sqrt{3}N$ and the angle between two forces will be $30{}^\circ$. Then what will be the value of the second force?

Answer 1

The square of the resultant force will be equivalent to the sum of the squares of each of the individual forces and product of the twice the both the forces and the cosine of the angle between the forces. This will help you in answering this question.

Complete step by step solution:
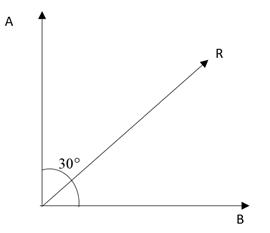
First of all let us mention what all are given in the question. The resultant of the two forces has been given as,
$R=10\sqrt{7}N$
One of the force has been given as,
$A=10\sqrt{3}N$
The angle between the forces are mentioned as,
$\theta =30{}^\circ$
As we all know the square of the resultant force will be equivalent to the sum of the squares of the each of the individual forces and product of the twice the both the forces and the cosine of the angle between the forces. This can be written as,
${{R}^{2}}={{A}^{2}}+{{B}^{2}}+2\times A\times B\times \cos \theta$
Where $B$ be the second force.
Substituting the values in it, we can write that,
${{\left( 10\sqrt{7} \right)}^{2}}={{\left( 10\sqrt{3} \right)}^{2}}+{{B}^{2}}+2\times 10\sqrt{7}\times B\times \cos 30{}^\circ$
Simplifying this equation can be shown as,
$\begin{aligned} & 700=300+{{B}^{2}}+2\times 10\sqrt{3}\times B\dfrac{\sqrt{3}}{2} \\\ & \Rightarrow 400={{B}^{2}}+30B \\\ \end{aligned}$
We can express this as a quadratic equation. That is,
${{B}^{2}}+30B-400=0$
The value of the force can be written as,
$B=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Substituting the values in this equation can be shown as,
$B=\dfrac{-30\pm \sqrt{900+4\times 400\times 1}}{2\times 1}=\dfrac{-30\pm \sqrt{2500}}{2}$
That is,
$B=\dfrac{-30\pm 50}{2}$
Therefore there will be two values for the forces which are given as,
$B=10N,-40N$
Therefore the answer for the question has been calculated.

Note:
In physics, a force has been mentioned as any interaction that will vary the motion of a body when it is unopposed. A force will result in a body with mass to vary its velocity. That means to accelerate the body. Force can also be explained simply as a push or a pull. This has been considered as a vector quantity.