Solveeit Logo
Login

Question

Question: The resultant of two forces acting at an angle of \({{120}^{\circ }}\)is 10 kg -wt and is perpendicu...

The resultant of two forces acting at an angle of 120∘{{120}^{\circ }}is 10 kg -wt and is perpendicular to one of the forces. That force is
A. 103kg−wt B. 203kg−wt C. 10kg-wt D. 103kg−wt \begin{aligned} & \text{A}\text{. 10}\sqrt{3}kg-wt \\\ & \text{B}\text{. 20}\sqrt{3}kg-wt \\\ & \text{C}\text{. 10kg-wt} \\\ & \text{D}\text{. }\dfrac{10}{\sqrt{3}}kg-wt \\\ \end{aligned}

Explanation

Solution

At first draw the figure as given in the question, Now we will use the parallelogram law to solve the question and according to this law, the resultant of two vector quantities that are represented in direction, magnitude, and sense by two sides of a parallelogram both of which are directed towards ow away from their point of interaction.

Complete step-by-step answer:

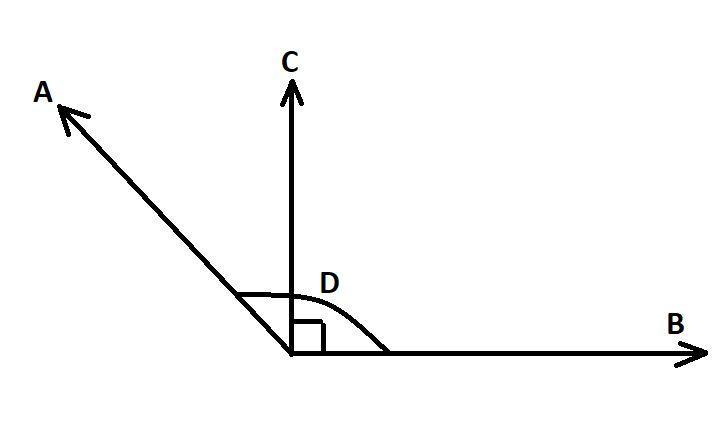
In the above diagram A and B are two forces acting from the same point and C is their resultant, the angle between the two forces A and B is 120∘{{120}^{\circ }}which is represented by D, and the angle between resultant for C and B is a right angle as it is given in the question that the angle between the resultant and one of the forces is a right angle. We have to find the force B.
Now, to find that we can shift the force A parallel without changing its direction, we can notice that if we shift force A parallel we can apply triangle law.

Now, we can figure out the triangle, and we can apply triangle law, one of the angle is 60∘{{60}^{\circ }}, as we know that the angle covered by D is 120∘{{120}^{\circ }}.
We know two of the angles of the triangle then the third angle must be, 30∘{{30}^{\circ }}, as we know that the sum of three angles of a triangle is 180∘{{180}^{\circ }}.
Now applying triangle law,
Or by using trigonometric ratios,
tan⁡θ=force that we need to findresultant force\tan \theta =\dfrac{\text{force that we need to find}}{\text{resultant force}}
tan⁡30∘=BC\tan {{30}^{\circ }}=\dfrac{B}{C} ,
C=Btan⁡30∘C=B\tan {{30}^{\circ }},
Now we know that the value of resultant force C is, 10kg-wt.
So,
C=10×13C=10\times \dfrac{1}{\sqrt{3}}.

So, the correct answer is “Option D”.

Note: While making the triangle trying to figure out the value of the unknown angles properly as the answer should solely depend on those angles. Students must know the values for ‘tan’ at some specific angles like 30, 60, 90, etc.