Question
Question: The resultant of two forces acting at an angle of \({{150}^{0}}\) is \(10kgwt\) and is perpendicular...
The resultant of two forces acting at an angle of 1500 is 10kgwt and is perpendicular to one of the forces. The smaller force is:
A. 103kgwt
B. 203kgwt
C. 20kgwt
D. 20/3kgwt
Solution
Hint: This problem can be solved by drawing a proper diagram with two coordinate axes and solving for the components of the force along these axes. The sum of the components of the two forces along each axis must be equal to the component of the resultant force along that axis.
Complete step-by-step answer:
Let us start off by drawing a proper diagram according to the information given in the question.
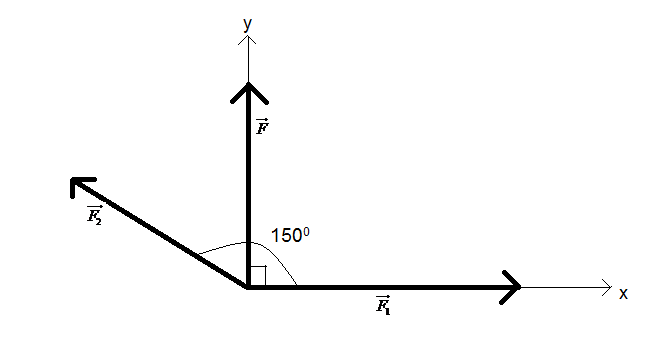
Let the two force vectors be F1 and F2 respectively. The resultant is F. Their orientation in the figure is according to the conditions given in the question. We have two coordinate axes x and y as shown in the figure. The sum of the components of the two forces along each axis must be equal to the component of the resultant force along that axis.
The magnitudes of F1, F2 and F are F1,F2 and F respectively.
Therefore solving the components along the x-axis we get,
F1+F2cos1500=Fcos900
∴F1+F2(−23)=F(0) (∵cos1500=−23,cos900=0)
∴F1−23F2=0
∴F1=23F2 --(1)
Now, solving the components along the y-axis we get, F1sin00+F2sin1500=F
∴F1(0)+F2(21)=F (∵sin00=0,sin1500=21)
∴0+21F2=F
∴21F2=F
∴F2=2F --(2)
Now, according to the question, F=10kgwt Putting this in (2), we get, ∴F2=2F=2×10=20kgwt --(3)
Putting (3) in (1), we get,
F1=23×20=103kgwt
Now, since 103<20, F1 is the smaller force.
Hence, the magnitude of the smaller force is 103kgwt.
Hence, the correct option is A) 103kgwt.
Note: This problem can be solved by using the cosine law for finding the magnitude of the resultant and equating it to the information given in the question. This gives us one equation. Another equation can be the formula for the angle of the resultant with respect to an individual vector which can also be equated with the help of the information given in the question. Hence, we will get two equations for two variables and can solve for the magnitudes of the individual forces respectively. Then we can check which force is the smaller one and that will be our required answer.
