Question

The resultant of three vectors 1, 2 and 3 units whose directions are those of the sides of an equilateral triangle taken in an order is at an angle of
$\text{A}\text{. 3}{{\text{0}}^{\text{0}}}\text{ with the first vector}$
$\text{B}\text{. 1}{{\text{5}}^{\text{0}}}\text{ with the first vector}$
$\text{C}\text{. 10}{{\text{0}}^{\text{0}}}\text{ with the first vector}$
$\text{D}\text{. 15}{{\text{0}}^{\text{0}}}\text{ with the first vector}$

Answer 1

First, arrange the three vectors with respect to the Cartesian plane. Resolve all the three vectors into their respective x and y components. The find the resultant vectors along x-axis and y-axis respectively.

Complete answer:
Let us first draw the vector diagram of the three given vectors. It is given that the directions of the three vectors are along the sides of an equilateral triangle. The vector diagram will be as given below.

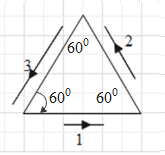
Let us rearrange the vectors and then draw them with respect to the Cartesian plane as shown below.

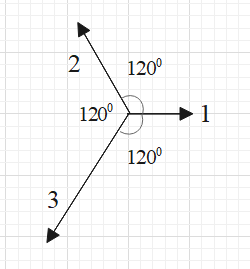
Resolve the vectors of 2 and 3 units into x and y components.
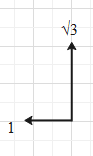
Here, the vector of 2 units is making an angle of 30$^{\text{0}}$ with the y-axis. Therefore, y component of the 2 unit vector will be $2\cos {{30}^{0}}=2\times \dfrac{\sqrt{3}}{2}=\sqrt{3}$ units in the upward direction. And the x component of this vector will be $2\sin {{30}^{0}}=2\times \dfrac{1}{2}=1$ units in the negative x-axis direction (towards left).

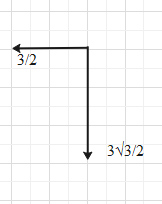
Here, the vector of 3 units is making an angle of 30$^{\text{0}}$ with the negative y-axis. Therefore, y component of the 3 unit vector will be $3\cos {{30}^{0}}=3\times \dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}$ units in the downwards direction. And the x component of this vector will be $3\sin {{30}^{0}}=3\times \dfrac{1}{2}=\dfrac{3}{2}$ units in the negative x-axis direction (towards left).

And the 1 unit vector is directed towards positive x-axis.

After resolving all the vectors into their x and y components we get,

As you can see, there are two vectors along the y-axis, $\sqrt{3}$ units upwards and $\dfrac{3\sqrt{3}}{2}$ units downwards. Therefore, the net vector in the upward direction (positive y-axis) is $\sqrt{3}-\dfrac{3\sqrt{3}}{2}=-\dfrac{\sqrt{3}}{2}$units. This means that the net vector along the y-axis is of $\dfrac{\sqrt{3}}{2}$units and in the negative y-axis direction.
There are three vectors along the x-axis, 1 plus $\dfrac{3}{2}$ units in the negative x-axis direction and 1 unit in the positive x-axis direction. Therefore, the net vector along the positive x-axis direction is $1-\left( 1+\dfrac{3}{2} \right)=-\dfrac{3}{2}$units. This means that the net vector along the x-axis is of $\dfrac{3}{2}$units and in the negative x-axis direction.
Hence, the vector diagram can be simplified to:

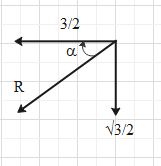
Now, let the resultant of these vectors be R and let it make an angle $\alpha$ with the negative x-axis.
From the above diagram we get that the magnitude of the resultant vector is,
$R=\sqrt{{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}+{{\left( \dfrac{3}{2} \right)}^{2}}}=\sqrt{\dfrac{3}{4}+\dfrac{9}{4}}=\sqrt{\dfrac{12}{4}}=\sqrt{3}$units
And $\cos \alpha =\dfrac{\dfrac{3}{2}}{R}=\dfrac{3}{2\sqrt{3}}=\dfrac{\sqrt{3}}{2}$.
We know that $\cos {{30}^{0}}=\dfrac{\sqrt{3}}{2}$.
Therefore, $\alpha ={{30}^{0}}$.

This means that the resultant vector makes an angle of ${{30}^{0}}$ with negative x-axis and we know that the vector of 1 unit is along the positive x-axis. Therefore, the resultant vector makes angle of ${{180}^{0}}-{{30}^{0}}={{150}^{0}}$ with the first vector.

So, the correct answer is “Option D”.

Note:
We can also find the resultant of the three vectors by the resultant formula for the resultant of two vectors.
i.e. $R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }$, where R, A and B are the magnitudes of the resultant, vector A and vector B respectively. $\theta$ is the angle between A and B.
First, find the resultant (R’) of vectors 2 and 3.
Then find the resultant of R’ and the vector of 1 unit.