Question
Question: The resultant of the three vectors, \(\overrightarrow {OM}\) and \(\overrightarrow {ON}\) shown in f...
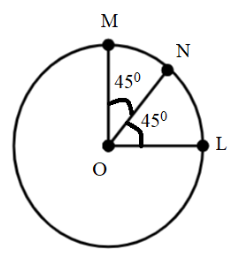
The resultant of the three vectors, OM and ON shown in figure is (Radius of the circle is r)
A. r(1−2) along ON
B. r(1+2) along OL
C. r(1+2) along ON
D. r(1−2) along OL
Solution
Vectors are quantities that consist of both magnitude and direction.The components along the X-axis and the Y-axis are considered in order to find out the resultant of the three vectors in accordance to each axis and then the total resultant is determined by summing up the total magnitude in each component for the three vectors.
Complete step by step answer:
The problem revolves around the concept of vectors and the reduction of a number of vectors by finding their resultant. In order to find the resultant of the three vectors we first need to know about what a resultant vector is. Resultant vectors are vectors that give the total magnitude of a number of vectors connected together. It is the result vector that is obtained by summing up the magnitudes of two or more vectors together. Here, we are asked to determine the resultant, that is, the total magnitude due to all the three vectors and in which direction the resultant vector is pointed toward.
It is given that the radius of the circle is r. Hence we can clearly see that the magnitudes of all these three vectors will be equivalent to the radius of the circle which is r because all these vectors extend from the center of the circle to a point on the circumference of the circle. Hence the magnitudes of all the three vectors are also said to be equal. Hence,
OL=OM ⇒OL=ON ⇒OL=r
Now we take each vector and find their magnitude and their corresponding direction with respect to the axis that is considered. We assume that the vectors are placed on the X-Y plane. This is done in order to know their directions. The directions are determined with the help of unit vectors, i^, j^ and k^ . We will be able to find the direction of each of these vectors.
The i^ unit vector denotes that the direction is along the X-axis, j^ unit vector denotes that the direction is along the Y-axis and k^ denotes that the direction is along the Z-axis. However the Z-axis is not required here as we consider the vectors to be present in a 2D plane, that is, a X-Y plane. We consider the X-components and Y-components of each vector separately in order to determine its magnitude and direction.
Let us first consider the vector OL. For this vector, we can see that the vector coincides with the X-axis hence making no angle with it. Since this vector is only along the X-axis, there is no Y-component that is present for it. Hence there is only a horizontal component which is denoted by the cosine angle, that is, the angle made with the X-axis.
Since there is only the cos component for vector OL we get:
OL=rcos0∘i^
Since, cos0∘=1 we get:
OL=ri^ --------(1)
Now let us consider vector OM. This vector coincides with the Y-axis hence making no angle with it. However the vector when considered from the X-axis, that is, with respect to the X-axis the angle will be 90∘ since it makes an angle of 90∘ with the X-axis. The vertical component is denoted by the sine angle for a vector.
Hence we get:
OM=rsin90∘j^
Since, sin90∘=1 we get:
OM=rj^ --------(2)
Let us now consider vector ON. This vector is said to be inclined at an angle which is given to be 45∘ and when a vector is said to be inclined at angle it is said to have both horizontal and vertical components. Hence, vector ON is given by both cosine and sine components which represent the horizontal and vertical components of a vector.
Hence, we get:
ON=rcos45∘i^+rsin45∘j^
By taking the common term rout we get:
ON=r[cos45∘i^+sin45∘j^]
Since, cos45∘=sin45∘=21 we get:
ON=r[21i^+21j^] ------(3)
As discussed earlier, we are required to find the resultant of the three vectors which is given by the sum of the three vector quantities. Let the resultant be denoted as Rnet. The resultant is hence given as:
Rnet=OL+OM+ON
Hence, by substituting the equations (1), (2) and (3) we get:
Rnet=ri^+rj^+r[21i^+21j^]
By solving further we get:
Rnet=ri^+rj^+2ri^+2rj^
The i^ components are added together separately while j^ components are added separately. Hence we get:
Rnet=[r+2r]i^+[r+2r]j^ -------(4)
Now we use a formula to find the magnitude of the resultant vector. When an equation is in the form:
R=xi^+yj^ where x and y are vectors then
This magnitude for resultant vector is given as:
R=x2+y2
By applying this formula from equation (4) we get:
Rnet=(r+2r)2+(r+2r)2
By further solving this we get:
Rnet=2(r+2r)2
⇒Rnet=2×(r+2r)2
⇒Rnet=2×(r+2r)
By taking the common term routside and expanding the brackets we get:
⇒Rnet=r(2+22)
⇒Rnet=r(1+2)
This is the final magnitude of the resultant vector. The direction of this resultant vector will be in the direction along the vector ON.
Hence, the correct option is option C.
Note: An alternative method which is used to find out the resultant is by considering the vectors OL and OM and finding out their resultant first. Their resultant will be along ON and hence this resultant and the vector ON are added up together since both will be of the same magnitude and direction, that is, along ON. The formula for calculating the magnitude of two vectors is applied to determine the magnitude of the resultant vector of vectors OL and OM.
