Question

The resultant magnetic moment of the following arrangement is:

                     ![](https://www.vedantu.com/question-sets/86e45fab-e298-4481-ab9c-c418aa51fd2a601552996515400518.png)   

A. M
B. 2M
C. 3M
D. 4M

Answer 1

In this question we can see that there are two different sets of the magnetic moments. In each set the magnetic moments are parallel to each other i.e. A is parallel to C and B is parallel to D. So, we will add these as they have the same direction and same magnitude. Later, we will be using the formula of parallelogram law of vector addition.
Formula used:
$R=\sqrt{{{a}^{2}}+{{b}^{2}}+2ab\cos \theta }$
Where,
The variable a and b represent the vectors and $\theta$is the angle between the vectors.

Complete answer:
As we can see, the magnetic moments A and C are parallel to each other. So, their net magnetic moment will be given as 2M in the same direction. Similarly, the other two vectors B and D are also parallel to each other, so their net magnetic moment is also given as 2M. Therefore, we have two magnetic moments as shown in figure (a).

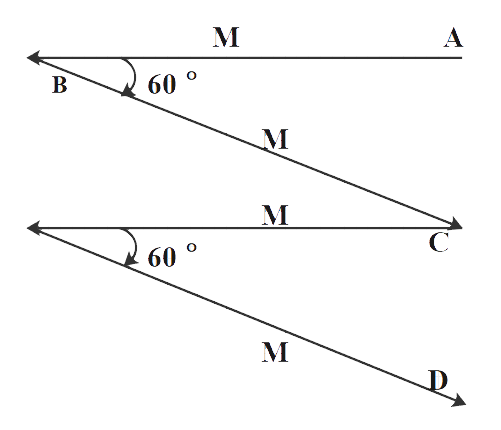
So, if we make these two magnetic vectors coplanar, we get vectors as shown in figure (b). The angle ($\theta$) between these moments is ${{180}^{{}^\circ }}-{{60}^{{}^\circ }}={{120}^{{}^\circ }}$as shown.
Now to find them we can use the parallelogram law of vector addition as the magnetic moment is a vector quantity.
We know the formula for parallelogram law of vector addition is,
$R=\sqrt{{{a}^{2}}+{{b}^{2}}+2ab\cos \theta }$
We have,
Vector a =b = 2M and $\theta ={{120}^{{}^\circ }}$
So, after substituting these above values in our equation
We get,
$R=\sqrt{{{\left( 2M \right)}^{2}}+{{\left( 2M \right)}^{2}}+2\left( 2M \right)\left( 2M \right)\cos \theta }$
$\therefore R=\sqrt{4{{M}^{2}}+4{{M}^{2}}+2\times 4{{M}^{2}}\times \left( -\dfrac{1}{2} \right)}$
On solving
We get,
$R=2M$

So, the correct answer is “Option B”.

Additional Information:
The direction of the resultant vector is not asked but in case it is asked we can find the angle ($\alpha$) between vector a and the resultant by using the formula $\tan \alpha =\dfrac{\sin \theta }{a+b\cos \theta }$

Note:
We can also solve this question by finding the resultant magnetic field between vector a and b. And then for c and d. We will then use the parallelogram law of vector addition and get the same result with different values. But, that would be confusing and time consuming.