Question
Question: The resultant magnetic moment for the following arrangement is: A. M B. 2M C. 3M D. 4M ![]...
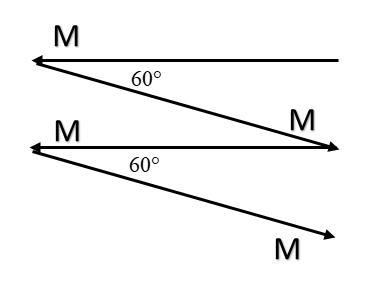
The resultant magnetic moment for the following arrangement is:
A. M
B. 2M
C. 3M
D. 4M
Solution
Magnetic field is the space around the magnet where the effect of magnet can be felt by another magnet or iron piece. Magnetic fields can also be produced by a moving charge whose intensity can be determined by the velocity and magnitude of charge or using a magnet having definite pole strength. The S.I unit of magnetic field is Tesla (T) whereas the C.G.S unit is Gauss (G).
Formula used:
R=A2+B2+2ABcosθ
Complete answer:
In physics, moment means the torque, if it is associated with some force. Hence magnetic moment is the measure of torque that a bar magnet will experience when placed in an external magnetic field. It is a vector quantity. Hence to get its resultant, we have to add it by vector addition.
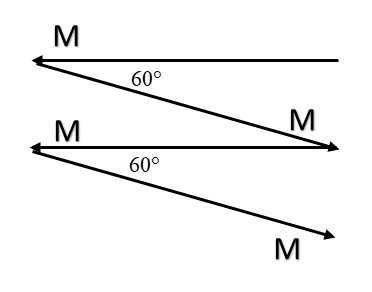
Now, using the property of vectors, we can displace the vector anywhere in the space by keeping its direction and magnitude the same. Now, the vectors which are present in the same direction could be simply added up. Thus we can redraw the diagram as:
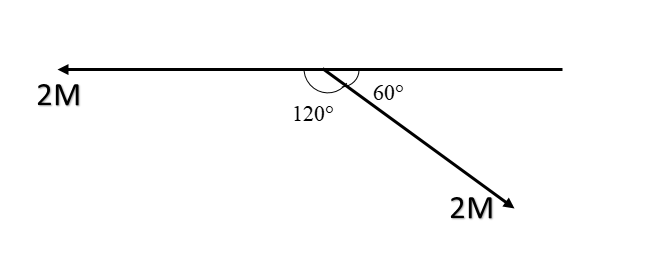
Here, by linear pair axiom, we can say the angles between two vectors as 180∘−60∘=120∘
Now, let the resultant of the moments be ‘R’ (as shown in the figure), hence we can use formulaR=A2+B2+2ABcosθ, we get:
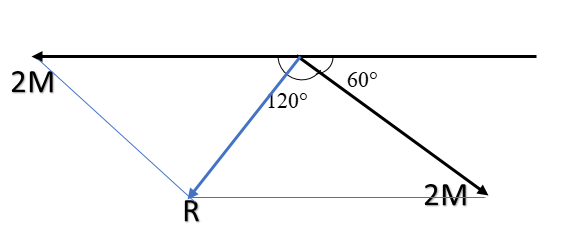
R=(2M)2+(2M)2+2(2M)(2M)cos120∘
R=4M2+4M2+8M2(2−1)
R=8M2−4M2
R=4M2=2M
Hence, the resultant equals 2M.
So, the correct answer is “Option B”.
Note:
In the above expression, we have the magnitude R=A2+B2+2ABcosθ, which has nothing to do with the direction of R i.e. resultant whereas in expression, α=tan−1Bcosθ+ABsinθ. The vector quantities can’t be expressed without its direction. Hence we can represent the resultant as 2M, making 60∘ with the horizontal.
