Question
Question: The resistances of three parts of a circular loop are as shown in the figure. The magnetic field at ...
The resistances of three parts of a circular loop are as shown in the figure. The magnetic field at the center O is (current enters at A and leaves at B and C as shown in the figure.)
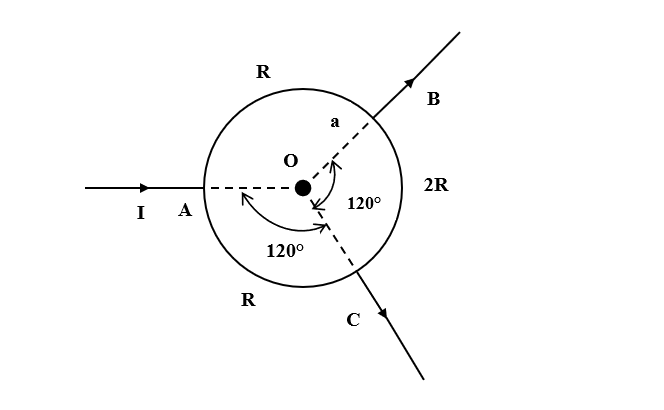
A. 6aμ0I
B. 3aμ0I
C. 32aμ0I
D. zero
Solution
From the figure we can say that the current I get equally divided between AB and AC. With the help of these currents find the potential difference across AB and AC. From the potential difference across AB and AC you will get the potential difference and the current flowing across BC. Then, use the formula for magnetic field and find the magnetic field due to AC, AB and BC. Adding the magnetic fields due to AB, AC and BC will give the net magnetic field. This obtained value will be the magnetic field at the center O.
Complete answer:
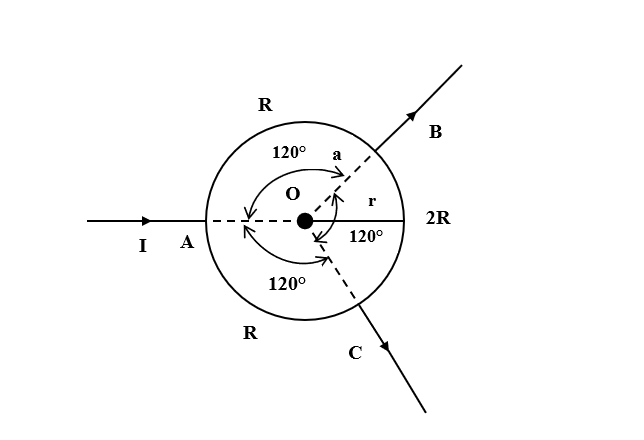
Let the radius of the circular loop be r
It is given that the current entering from A is I.
The circuit is symmetric so the current flowing from A to B will be equal to the current flowing from A to C.
Current from A to B= Current from A to C= 2I
Let the potential at A be VA
Similarly, at B and C be VB and VC respectively.
The potential difference between A and B can be given by,
VB−VA=2IR
⇒VB=VA+2IR …(1)
Similarly, the potential difference between A and C can be given by,
VC−VA=2IR
⇒VC=VA+2IR …(2)
From the equation. (1) and (2) we get,
VB=VC
Thus, as the potential at B and C are the same, no current will flow from B to C.
We know, Magnetic field is given by,
B=360°θ.2πrμ0I
Magnetic field due to AC by substituting the values in above equation is given by,
BAC=360°120°.4πrμ0I
⇒BAC=31.4πrμ0I
Now, applying the right hand thumb rule, the direction of the magnetic field is outwards.
Similarly, Magnetic field due to AB is given by,
BAB=360°120°.4πrμ0I
⇒BAB=31.4πrμ0I
Applying right hand thumb rule, the magnetic field due to AB is inwards.
Similarly, Magnetic field due to BC is given by,
BBC=360°120°.2πrμ0×0
⇒BBC=0
The magnitude of the magnetic field due to AB and AC are the same but their direction is opposite.
⇒BAC=−BAB …(3)
Thus, the net magnetic field is given by,
Bnet=BAC+BAB+BBC
Substituting equation. (3) and value of BBC in above equation we get,
Bnet=−BAB+BAB+0
⇒Bnet=0
Thus, the magnetic field at the center O is zero.
So, the correct answer is option D i.e. zero.
Note:
For solving this question, we have used the right hand thumb rule. Students should not get confused between the right-hand thumb rule and Fleming’s right hand rule. According to Fleming’s right hand rule, the thumb indicates the direction of force, the forefinger indicates the direction of the magnetic field and the middle finger represents the direction of current. Whereas according to right hand thumb rule, the thumb indicates the direction of current and the direction in which the fingers wrap gives the direction of magnetic field.
